
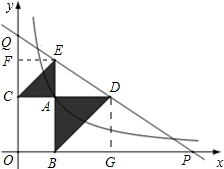
 的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x轴于点P,Q.当QE:DP=4:9时,图中阴影部分的面积等于 .
的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x轴于点P,Q.当QE:DP=4:9时,图中阴影部分的面积等于 .
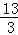
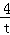 ),则AD=AB=DG=
),则AD=AB=DG=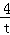 ,AE=AC=EF=t,则图中阴影部分的面积=△ACE的面积+△ABD的面积=
,AE=AC=EF=t,则图中阴影部分的面积=△ACE的面积+△ABD的面积= t2+
t2+ ×
×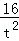 ,因此只需求出t2的值即可.先在直角△ADE中,由勾股定理,得出DE=
,因此只需求出t2的值即可.先在直角△ADE中,由勾股定理,得出DE=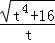 ,再由△EFQ∽△DAE,求出QE=
,再由△EFQ∽△DAE,求出QE=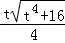 ,△ADE∽△GPD,求出DP=:
,△ADE∽△GPD,求出DP=: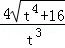 ,然后根据QE:DP=4:9,即可得出t2=
,然后根据QE:DP=4:9,即可得出t2= .
.
 ),则AD=AB=DG=
),则AD=AB=DG= ,AE=AC=EF=t.
,AE=AC=EF=t.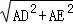 =
=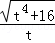 .
.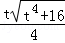 ,
,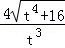 .
.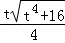 :
: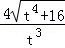 =4:9,
=4:9,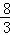 .
. AC2+
AC2+ AB2=
AB2= t2+
t2+ ×
×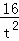 =
=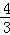 +3=
+3=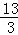 .
. ),
), ,DG=
,DG= ,GP="9t"
,GP="9t"  =
= :9t,即t2=
:9t,即t2=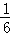 ,
,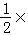 4t×4t+
4t×4t+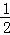 ×
× ×
× =
= .
. .
.

科目:初中数学 来源:不详 题型:解答题
 (x>0)与正比例函数y=k2x的图象分别交矩形OABC的BC边于M(4,1),B(4,5)两点.
(x>0)与正比例函数y=k2x的图象分别交矩形OABC的BC边于M(4,1),B(4,5)两点.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 x﹣1与反比例函数
x﹣1与反比例函数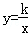 (x<0)的图象交于点A,与x轴相交于点B,过点B作x轴垂线交双曲线于点C,若AB=AC,则k的值为( )
(x<0)的图象交于点A,与x轴相交于点B,过点B作x轴垂线交双曲线于点C,若AB=AC,则k的值为( )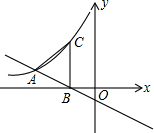
| A.﹣2 | B.﹣4 | C.﹣6 | D.﹣8 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 )处,两直角边分别与x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+
)处,两直角边分别与x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+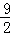 与双曲线y=
与双曲线y= (m>0)的交点.
(m>0)的交点.
 (m>0)在A,B之间的部分为L,让一把三角尺的直角顶点P在L上滑动,两直角边始终与坐标轴平行,且与线段AB交于M,N两点,请探究是否存在点P使得MN=
(m>0)在A,B之间的部分为L,让一把三角尺的直角顶点P在L上滑动,两直角边始终与坐标轴平行,且与线段AB交于M,N两点,请探究是否存在点P使得MN= AB,写出你的探究过程和结论.
AB,写出你的探究过程和结论.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
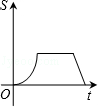
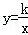 (k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C.动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C.过P作PM⊥x轴,PN⊥y轴,垂足分别为M、N.设四边形OMPN的面积为S,P点运动时间为t,则S关于t的函数图象大致为( )
(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C.动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C.过P作PM⊥x轴,PN⊥y轴,垂足分别为M、N.设四边形OMPN的面积为S,P点运动时间为t,则S关于t的函数图象大致为( )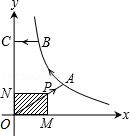
 B.
B.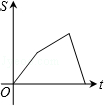 C.
C.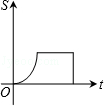 D.
D.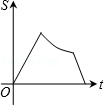
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 (k>0)与一次函数
(k>0)与一次函数 (b>0)的图像相交于两点
(b>0)的图像相交于两点 ,线段AB交y轴于点C,当
,线段AB交y轴于点C,当 且AC=2BC时,k、b的值分别为( ).
且AC=2BC时,k、b的值分别为( ).A.k= ,b=2 ,b=2 | B.k= ,b=1 ,b=1 | C.k= ,b= ,b= | D.k= ,b= ,b= |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com