
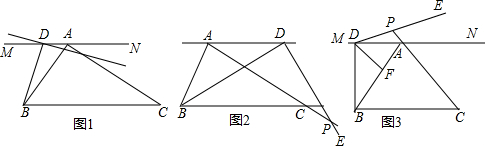
分析 (1)如图1,作辅助线,构建全等三角形,证明△BDF≌△PDA,可得结论;
(2)如图2,作辅助线,同理证明△DAB≌△DFP,可得BD=PD;
(3)如图3,同理作辅助线,证明△BDG≌△PDA,可得BD=PD;
如图4,根据△BDG≌△PDA,得AP=BG,并由等腰三角形ADG的三线合一得:AG=2AF,从而根据线段的和得出结论.
解答  证明:(1)如图1,过D作DF⊥MN,交AB于F,
证明:(1)如图1,过D作DF⊥MN,交AB于F,
∴∠ADF=90°,
∵∠BAC=90°,AB=AC,
∴∠ABC=45°,
∵MN∥BC,
∴∠MAB=∠ABC=45°,
∴△ADF是等腰直角三角形,
∴AD=DF,
∵∠BDE=90°,
∴∠BDF+∠FDP=90°,
∵∠ADP+∠FDP=90°,
∴∠BDF=∠ADP,
∵∠BFD=180°-∠DFA=180°-45°=135°,
∠DAC=∠DAF+∠BAC=45°+90°=135°,
∴∠BFD=∠DAC,
∴△BDF≌△PDA,
∴BD=PD;
(2)BD=PD仍然成立,理由是:
如图2,过D作DF⊥MN,交AC于F,则∠ADF=90°,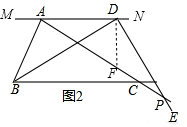
∵MN∥BC,
∴∠DAF=∠ACB=45°,
∴△ADF是等腰直角三角形,
∴AD=DF,
∵∠PDF+∠BDF=90°,
∠ADB+∠BDF=90°,
∴∠PDF=∠ADB,
∵∠PFD=180°-45°=135°,
∠BAD=90°+45°=135°,
∴∠PFD=∠BAD,
∴△DAB≌△DFP,
∴BD=PD;
(3)如图3,BD=PD,理由是:
过D作DG⊥MN,交AB的延长线于G,
同理得△ADG是等腰直角三角形,
∴AD=DG,
∵∠GDB+∠BDA=90°,
∠PDA+∠BDA=90°,
∴∠GDB=∠PDA,
∵∠DGA=∠DAG=45°,∠BAC=90°,
∴∠PAM=180°-∠BAC-∠DAG=45°,
∴∠PAM=∠DGA,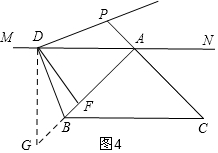
∴△BDG≌△PDA,
∴BD=PD;
如图4,∵AD=DG,DF⊥AG,
∴AG=2AF,
∵△BDG≌△PDA,
∴AP=BG,
∵AG=AB+BG,
∴AG=AB+AP,
∴AP+AB=2AF.
点评 本题是三角形的综合题,难度适中,考查了等腰直角三角形、全等三角形的性质和判定,在证明三角形全等的条件中,常利用同角的余角相等来证明两角相等,本题的三个问题的证明思路类似:都是作MN的垂线,证明△DAB≌△DFP,得出结论.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
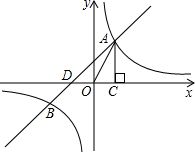 如图,已知反比例函数y1=$\frac{{k}_{1}}{x}$(k1>0)与一次函数y2=k2x+1(k2≠0)的图象交于A,B两点,AC⊥x轴于点C.若△OAC的面积为1,且AC=2OC.
如图,已知反比例函数y1=$\frac{{k}_{1}}{x}$(k1>0)与一次函数y2=k2x+1(k2≠0)的图象交于A,B两点,AC⊥x轴于点C.若△OAC的面积为1,且AC=2OC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=-x+4的图象与反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于点A(1,a),B两点.求反比例函数的表达式及点B的坐标.
如图,一次函数y=-x+4的图象与反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于点A(1,a),B两点.求反比例函数的表达式及点B的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 算筹是我国古代的计算工具之一,也是中华民族智慧的结晶,如图1中用算筹表示的算式是“7408+2366”,则图2中算筹表示的算式的运算结果为-426.
算筹是我国古代的计算工具之一,也是中华民族智慧的结晶,如图1中用算筹表示的算式是“7408+2366”,则图2中算筹表示的算式的运算结果为-426.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,如图,△ABC是直角三角形,∠ACB=90°,∠ABC=60°,BC=6cm,点P由C开始向点B以1cm/s的速度运动,点Q由B开始向点A以2cm/s的速度运动,若PQ同时开始运动
已知,如图,△ABC是直角三角形,∠ACB=90°,∠ABC=60°,BC=6cm,点P由C开始向点B以1cm/s的速度运动,点Q由B开始向点A以2cm/s的速度运动,若PQ同时开始运动查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com