
【题目】已知四边形ABCD中,AD+DB+BC=16,则四边形ABCD的面积的最大值是( )
A. 16 B. 32 C. 16![]() D.
D. ![]()
【答案】B
【解析】先画图,由于S四边形ABCD=S△ABD+S△BCD,那么当∠ADB=∠BCD=90°时,S△ABD、S△BCD有最大值,也就是四边形ABCD有最大值,再结合AD+DB+BC=16,可求S四边形ABCD=8BD-![]() BD2,再利用二次函数的求最值问题,即可求四边形ABCD的面积.
BD2,再利用二次函数的求最值问题,即可求四边形ABCD的面积.
解:如图所示,连接BD,
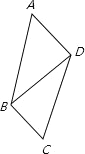
∵S四边形ABCD=S△ABD+S△BCD,
S△ABD=![]() ADBDsin∠ADB,
ADBDsin∠ADB,
S△BCD=![]() BDBCsin∠BCD,
BDBCsin∠BCD,
∴当∠ADB=∠BCD=90°时,S△ABD、S△BCD有最大值,
∴S四边形ABCD=S△ABD+S△BCD=![]() ADBD+
ADBD+![]() BDBC,
BDBC,
又∵AD+BC=16-BD,
∴S四边形ABCD=![]() BD(16-BD)=8BD-
BD(16-BD)=8BD-![]() BD2,
BD2,
∵a=-![]() <0,
<0,
∴当BD=-![]() =8时,四边形ABCD的面积有最大值=
=8时,四边形ABCD的面积有最大值=![]() =32.
=32.
故四边形ABCD的最大面积是32.
“点睛”本题考查了四边形面积的计算、二次函数的性质.已知两边和夹角,可利用夹角的正弦来求面积.要使三角形面积最大,则夹角应等于90°.


 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中有红球和黑球共25个,这些球除颜色外都相同.进行大量的摸球试验(每次摸出1个球)后,发现摸到黑球的频率在0.6附近摆动,据此可以估计黑球为___个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A(1,2),B(3,1),C(﹣2,﹣1). 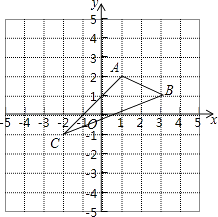
(1)在图中作出△ABC关于y轴的对称△A1B1C1;
(2)写出△ABC关于x轴对称△A2B2C2的各顶点坐标:
A2;
B2;
C2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小军和小颖对小区学生早上上学到校方式进行了调查,小军将调查结果整理后绘制成如图条形统计图,A代表自行车,B代表步行,C代表乘车. 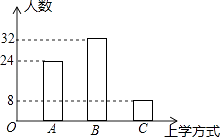
(1)小军和小颖一共调查了多少人?
(2)小颖想将调查结果绘制成扇形统计图,求扇形统计图中C部分对应的扇形的圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答
(1)如图1,已知数轴上有三点A,B,C,点B是线段AC的中点. 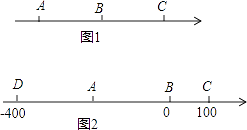
若点A对应的数是3,点C对应的数是9,则点B对应的数是;
若点A对应的数是﹣11,点C对应的数是﹣5,则点B对应的数是;
若点A对应的数是﹣2,点C对应的数是8,则点B对应的数是;
(2)在(1)的条件下,若点A对应的数是x,点C对应的数是y,请你猜想:线段AC的中点B对应的数是(用含x,y的代数式表示).
(3)如图2,在数轴上,若点D,B,C对应的数分别是﹣400,0,100,点A是线段DB的中点,动点、Q分别从D、B两点同时出发沿数轴向左运动,点P、Q的速度分别为10单位长度/秒、5单位长度/秒,点M为线段PQ的中点,在上述运动过程中, ![]() QC﹣AM的值是否发生变化?若不变,求其值;若改变,请说明理由.
QC﹣AM的值是否发生变化?若不变,求其值;若改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求完成作图,并回答问题;如图在△ABC中:
(1)过点A画BC的垂线,垂足为E;
(2)画∠ABC的平分线,交AC于F;
(3)过E画AB的平行线,交AC于点G;
(4)过点C画AB所在的直线的垂线段,垂足为H.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com