
【题目】随着移动计算技术和无线网络的快速发展,移动学习方式越来越引起人们的关注.某校计划将这种学习方式应用到教育教学中,从各年级共1500名学生中随机抽取了部分学生,对其家庭中拥有的移动设备情况进行了调查,并绘制出如下的统计图①和图②,根据相关信息,解答下列问题:
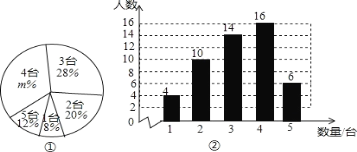
(1)本次接受随机抽样调查的学生人数为 人 ,图①中m的值为 .
(2)求本次调查获取的样本数据的众数、中位数;
(3)根据样本数据,估计该校学生家庭中;拥有3台移动设备的学生人数.
【答案】(1)50,32;(2)众数为4;中位数是3;(3)420
【解析】
(1)根据2台的人数和所占百分比可求出调查的学生总人数,用4台的人数除以总人数可得m的值;
(2)根据众数和中位数的定义求解;
(3)用1500乘以拥有3台移动设备的学生人数所占的百分比即可.
解:(1)本次接受随机抽样调查的学生人数为:10÷20%=50(人),![]() ,
,
∴m=32,
故答案为:50,32;
(2)∵这组样本数据中,4出现了16次,出现次数最多,
∴这组数据的众数为4;
∵将这组数据从小到大排列,其中处于中间的两个数均为3,且![]() =3,
=3,
∴这组数据的中位数是3;
(3)1500×28%=420(人),
答:估计该校学生家庭中;拥有3台移动设备的学生人数约为420人.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】丽君花卉基地出售两种盆栽花卉:太阳花6元/盆,绣球花10元/盆.若次购买的绣球花超过20盆时,超过20盆部分的绣球花价格打8折.
(1)求出太阳花的付款金额![]() (元)关于购买量
(元)关于购买量![]() (盆)的函数关系式;
(盆)的函数关系式;
(2)求出绣球花的付款金额![]() (元)关于购买量
(元)关于购买量![]() (盆)的函数关系式;
(盆)的函数关系式;
(3)为了美化环境,花园小区计划到该基地购买这两种花卉共90盆,其中太阳花数量不超过绣球花数量的一半.两种花卉各买多少盆时,总费用最少,最少费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
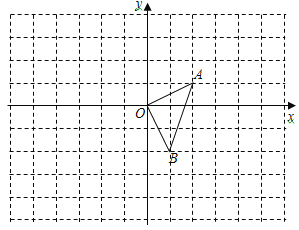
【题目】(8分)如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0)、A(2,1)、B(1,-2).
(1)以原点O为位似中心,在y轴的右侧画出△OAB的一个位似△OA1B1 ,使它与△OAB的相似比为2:1,并分别写出点A、B的对应点A1、B1的坐标.
(2)画出将△OAB向左平移2个单位,再向上平移1个单位后的△O2A2B2 ,并写出点A、B的对应点A2、B2的坐标.
(3)判断△OA1B1与△O2A2B2 ,能否是关于某一点M为位似中心的位似图形,若是,请在图中标出位似中心M,并写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一块三角板放在直角坐标系第一象限内,其中30°角的顶点A落在y轴上,直角顶点C落在x轴的(![]() ,0)处,∠ACO=60°,点D为AB边上中点,将△ABC沿x轴向右平移,当点A落在直线y=x﹣3上时,线段CD扫过的面积为_____.
,0)处,∠ACO=60°,点D为AB边上中点,将△ABC沿x轴向右平移,当点A落在直线y=x﹣3上时,线段CD扫过的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读资料:小明是一个爱动脑筋的好学生,他在学习了有关圆的切线性质后,意犹未尽,又查阅到了与圆的切线相关的一个问题:
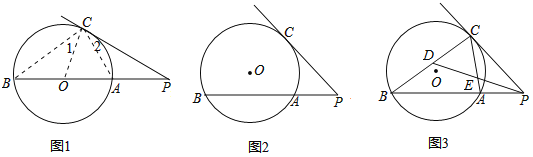
如图1,已知PC是⊙O的切线,AB是⊙O的直径,延长BA交切线PC与P,连接AC、BC、OC.
因为PC是⊙O的切线,AB是⊙O的直径,所以∠OCP=∠ACB=90°,所以∠1=∠2.
又因为∠B=∠1,所以∠B=∠2.
在△PAC与△PCB中,又因为:∠P=∠P,所以△PAC∽△PCB,所以![]() ,即PC2=PAPB.
,即PC2=PAPB.
问题拓展:
(Ⅰ)如果PB不经过⊙O的圆心O(如图2)等式PC2=PAPB,还成立吗?请证明你的结论;
综合应用:
(Ⅱ)如图3,⊙O是△ABC的外接圆,PC是⊙O的切线,C是切点,BA的延长线交PC于点P;
(1)当AB=PA,且PC=12时,求PA的值;
(2)D是BC的中点,PD交AC于点E.求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与AC相交于点E.
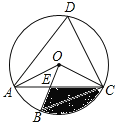
(1)求∠OCA的度数;
(2)若∠COB=3∠AOB,OC=![]() ,求图中阴影部分面积(结果保留π和根号).
,求图中阴影部分面积(结果保留π和根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店计划购进![]() ,
,![]() 两种型号的电机,其中每台
两种型号的电机,其中每台![]() 型电机的进价比
型电机的进价比![]() 型多
型多![]() 元,且用
元,且用![]() 元购进
元购进![]() 型电机的数量与用
型电机的数量与用![]() 元购进
元购进![]() 型电机的数量相等.
型电机的数量相等.
(1)求![]() ,
,![]() 两种型号电机的进价;
两种型号电机的进价;
(2)该商店打算用不超过![]() 元的资金购进
元的资金购进![]() ,
,![]() 两种型号的电机共
两种型号的电机共![]() 台,至少需要购进多少台
台,至少需要购进多少台![]() 型电机?
型电机?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道“距离地面越高,温度越低”,下表给出了距离地面的高度与所在位置的温度之间的大致关系.
距离地面的高度(千米) | 0 | 1 | 2 | 3 | 4 | 5 |
所在位置的温度(C) | 20 | 14 | 8 | 2 |
|
|
(1)上表中哪个是自变量?
(2)由表可知,距离地面高度每上升1千米,温度降低______℃;
(3)2018年5月14日,四川航空3U8633航班执行重庆—拉萨航班任务,飞行途中,在距离地面9800米的高空,驾驶舱右侧挡风玻璃突然破裂,2名飞行员在超低压、超低温的紧急情况下,冷静应对,最终飞机成功降落,创造了世界航空史上的奇迹,请你计算出飞机发生事故时所在高空的温度(假设当时所在位置的地面温度为20℃).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com