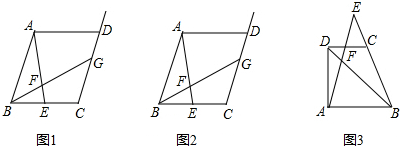
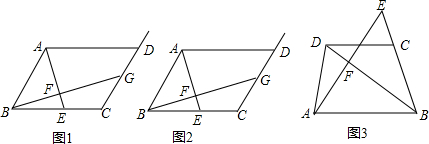
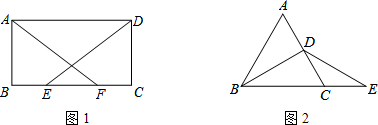
解:(1)由图②可知点P从A点运动到B点的时间为10s,
又因为P点运动的速度为1cm/s,
所以AB=10×1=10(cm),
而AD=9cm,
则平行四边形ABCD的周长为:2(AB+AD)=2(10+9)=38(cm);

(2)线段MN表示的实际意义是:点P在BC边上从B点运动到C点;
(3)由AD=9可知点P在边BC上的运动时间为9s,
所以a=10+9=19;
分别过B点、C两点作BE⊥AD于E,CF⊥AD于F.
由图②知S
△ABD=36,
则

×9×BE=36,
解得BE=8,
在直角△ABE中,由勾股定理,得AE=

=6.
易证△BAE≌△CDF,
则BE=CF=8,AE=DF=6,AF=AD+DF=9+6=15.
在直角△ACF中,由勾股定理,得CA=
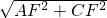
=17,
则点P在CA边上从C点运动到A点的时间为17s,
所以b=19+17=36.
分析:(1)由图②知点P在AB上运动的时间为10s,根据列出=速度×时间,求出AB=10cm,又AD=9cm,根据平行四边形的周长公式即可求解;
(2)由线段MN∥x轴,可知此时点P虽然在运动,但是△PAD的面积y不变,结合图①,可知此时点P在BC边上运动;
(3)由AD=9可知点P在边BC上的运动时间为9s,a为点P由A→B→C的时间;分别过B点、C点作BE⊥AD、CF⊥AD,易证△BAE≌△CDF,由此得到AE=DF=6,AF=15,从而可求得CA=17s,则点P在CA边上从C点运动到A点的时间为17,所以b=19+17=36.
点评:本题考查了动点问题的函数图象,根据图②的三角形的面积的变化情况求出AB的长度是解题的关键,在梯形的问题中,作梯形的高是一种常用的辅助线的作法.


 (2)线段MN表示的实际意义是:点P在BC边上从B点运动到C点;
(2)线段MN表示的实际意义是:点P在BC边上从B点运动到C点; ×9×BE=36,
×9×BE=36, =6.
=6.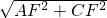 =17,
=17,