已知一次函数y=kx+b的图象如图所示,则k,b的符号是 ( )A．k＞0.b＞0B．k＞0.b＜0C．k＜0.b＞0D．k＜0.b＜0 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

已知一次函数y=kx+b的图象如图所示,则k,b的符号是 ( )

A．k＞0，b＞0

B．k＞0，b＜0

C．k＜0，b＞0

D．k＜0，b＜0

试题分析：由一次函数y=kx+b的图象经过二、三、四象限，
又有k＜0时，直线必经过二、四象限，故知k＜0，
再由图象过三、四象限，即直线与y轴负半轴相交，所以b＜0．
故选D．

练习册系列答案

每时每课期中期末课时单元系列答案

全优考典单元检测卷及归类总复习系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源：不详 题型：解答题

下表中，y是x的一次函数．

x	2	1	2		5
y	6	3		12	15

（1）求该函数的表达式，并补全表格；
（2）已知该函数图象上一点M（1，-3）也在反比例函数

图象上，求这两个函数图象的另一交点N的坐标．

查看答案和解析>>

科目：初中数学 来源：不详 题型：解答题

设p,q都是实数，且

．我们规定：满足不等式

的实数x的所有取值的全体叫做闭区间，表示为

．对于一个函数，如果它的自变量x与函数值y满足：当

时，有

，我们就称此函数是闭区间

上的“闭函数”．
（1）反比例函数

是闭区间

上的“闭函数”吗？请判断并说明理由；
（2）若一次函数

是闭区间

上的“闭函数”，求此函数的解析式；
（3）若实数c，d满足

，且

，当二次函数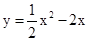

是闭区间

上的“闭函数”时，求c，d的值．

查看答案和解析>>

科目：初中数学 来源：不详 题型：填空题

点A（3，

）和点B（-2，

）都在直线y=-4x+1上，则

，

的大小关系是（）
（选填“>”“＝”“<”）。

查看答案和解析>>

科目：初中数学 来源：不详 题型：解答题

在购买某场足球赛门票时，设购买门票数为x（张），总费用为y（元）．现有两种购买方案：
方案一：若单位赞助广告费10000元，则该单位所购门票的价格为每张60元；
（总费用＝广告赞助费+门票费）
方案二：购买门票方式如图所示．
解答下列问题：
（1）方案一中，y与x的函数关系式为     ；
方案二中，当0≤x≤100时，y与x的函数关系式为     ，
当x＞100时，y与x的函数关系式为        ；
（2）如果购买本场足球赛门票超过100张，你将选择哪一种方案，使总费用最省？请说明理由；
（3）甲、乙两单位分别采用方案一、方案二购买本场足球赛门票共700张，花去总费用计58000元，求甲、乙两单位各购买门票多少张．