
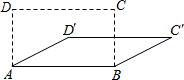
 将四根木条钉成的长方形木框变形为平行四边形ABCD的形状,并使其面积为长方形面积的$\frac{\sqrt{2}}{2}$倍(木条宽度忽略不计),则这个平行四边形的最小内角为45度.
将四根木条钉成的长方形木框变形为平行四边形ABCD的形状,并使其面积为长方形面积的$\frac{\sqrt{2}}{2}$倍(木条宽度忽略不计),则这个平行四边形的最小内角为45度. 分析 平行四边形ABCD的面积等于矩形面积的$\frac{\sqrt{2}}{2}$.且它们的底相等,所以平行四边形ABCD的高等于矩形高的$\frac{\sqrt{2}}{2}$.过点C作AB的垂线垂足是E,运用三角函数求解即可.
解答 解:过点C作AB的垂线垂足是E,如图所示: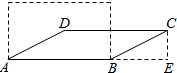
∵将四根木条钉成的矩形木框变形为平行四边形木框ABCD的形状,并使其面积为矩形木框的$\frac{\sqrt{2}}{2}$,
∴BC=$\sqrt{2}$CE,
∵sin∠CBE=$\frac{CE}{BC}$=$\frac{\sqrt{2}}{2}$,
∴∠CBE=∠A=45°.
故答案为:45.
点评 本题考查了矩形的性质、平行四边形的性质、面积的计算、三角函数的运用;通过作辅助线构造直角三角形,运用三角函数是解决问题的关键.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
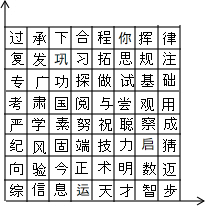 如图是一组密码的一部分,为了保密,许多情况下课采用不同的密码,请你运用所学知识找到破译的“钥匙”.目前,已破译出“正做数学”的真实意思是“祝你成功”.若“正”所处的位置为(x,y),你找到的密码钥匙是对应文字横坐标加1,纵坐标加2,破译的“今天考试”真实意思是“努力发挥”.
如图是一组密码的一部分,为了保密,许多情况下课采用不同的密码,请你运用所学知识找到破译的“钥匙”.目前,已破译出“正做数学”的真实意思是“祝你成功”.若“正”所处的位置为(x,y),你找到的密码钥匙是对应文字横坐标加1,纵坐标加2,破译的“今天考试”真实意思是“努力发挥”.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com