
【题目】四边形![]() 为正方形,点
为正方形,点![]() 为线段
为线段![]() 上一点,连接
上一点,连接![]() ,过点
,过点![]() 作
作![]() ,交射线
,交射线![]() 于点
于点![]() ,以
,以![]() 、
、![]() 为邻边作矩形
为邻边作矩形![]() ,连接
,连接![]() .
.
(1)如图,求证:矩形![]() 是正方形;
是正方形;

(2)当线段![]() 与正方形
与正方形![]() 的某条边的夹角是
的某条边的夹角是![]() 时,求
时,求![]() 的度数.
的度数.
【答案】∠EFC=125°或145°.
【解析】
(1)首先作EP⊥CD于P,EQ⊥BC于Q,由∠DCA=∠BCA,得出EQ=EP,再由∠QEF+∠FEC=45°,得出∠PED+∠FEC=45°,进而得出∠QEF=∠PED,即可判定Rt△EQF≌Rt△EPD,得出EF=ED,即可得证;
(2)分类讨论:①当DE与AD的夹角为35°时,∠EFC=125°;②当DE与DC的夹角为35°时,∠EFC=145°,即可得解.
(1)作EP⊥CD于P,EQ⊥BC于Q,如图所示
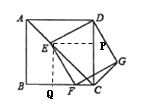
∵∠DCA=∠BCA
∴EQ=EP,
∵∠QEF+∠FEP=90°,∠PED+∠FEP=90°,
∴∠QEF=∠PED
在Rt△EQF和Rt△EPD中,
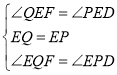
∴Rt△EQF≌Rt△EPD
∴EF=ED
∴矩形DEFG是正方形;
(2)①当DE与AD的夹角为35°时,
∠DEP=∠QEF=35°,
∴∠EFQ=90°-35°=55°,
∠EFC=180°-55°=125°;
②当DE与DC的夹角为35°时,
∠DEP=∠QEF=55°,
∴∠EFQ=90°-55°=35°,
∠EFC=180°-35°=145°;
综上所述,∠EFC=125°或145°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列关于函数![]() 的四个命题:①当
的四个命题:①当![]() 时,
时, ![]() 有最小值10;②
有最小值10;②![]() 为任意实数,
为任意实数, ![]() 时的函数值大于
时的函数值大于![]() 时的函数值;③若
时的函数值;③若![]() ,且
,且![]() 是整数,当
是整数,当![]() 时,
时, ![]() 的整数值有
的整数值有![]() 个;④若函数图象过点
个;④若函数图象过点![]() 和
和![]() ,其中
,其中![]() ,
, ![]() ,则
,则![]() .其中真命题的序号是( )
.其中真命题的序号是( )
A. ① B. ② C. ③ D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() 在直线
在直线![]() 上,射线
上,射线![]() 在直线
在直线![]() 的上方,且
的上方,且![]()
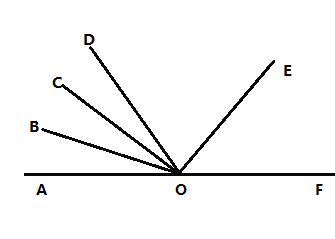
(1)如图1,![]() 在
在![]() 内部,且
内部,且![]() 平分
平分![]()
①若![]() =
=![]() ,则
,则![]() = .
= .
②若![]() =
=![]() ,则
,则![]() = .
= .
③若![]() =
=![]() ,则
,则![]() = °(用含
= °(用含![]() 的式子表示)
的式子表示)
(2)当![]() 在
在![]() 内部,且
内部,且![]() 平分
平分![]() 时,请画出图形;此时,
时,请画出图形;此时,![]() 与
与![]() 有怎样的数量关系?请说明理由.
有怎样的数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超速行驶是引发交通事故的主要原因.上周末,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在到永丰路的距离为100米的点P处.这时,一辆小轿车由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为4秒,![]() ,
,![]() .
.
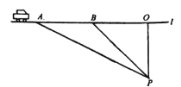
(1)求A、B之间的路程;
(2)请判断此车是否超过了永丰路每小时54千米的限制速度?(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
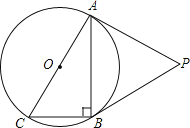
【题目】如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是⊙O外一点,PA切⊙O于点A,且PA=PB.
(1)求证:PB是⊙O的切线;
(2)已知PA=2![]() ,BC=2.求⊙O的半径.
,BC=2.求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列的解题过程,然后回答下列问题.
例:解绝对值方程:![]() .
.
解:讨论:①当![]() 时,原方程可化为
时,原方程可化为![]() ,它的解是
,它的解是![]() ;
;
②当![]() 时,原方程可化为
时,原方程可化为![]() ,它的解是
,它的解是![]() .
.
原方程的解为![]() 或
或![]() .
.
(1)依例题的解法,方程算![]() 的解是_______;
的解是_______;
(2)尝试解绝对值方程:![]() ;
;
(3)在理解绝对值方程解法的基础上,解方程:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
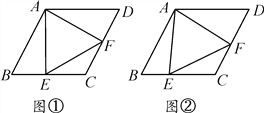
【题目】菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.
(1)如图①,若点E是BC的中点,∠AEF=60°,求证:BE=DF;
(2)如图②,若∠EAF=60°,求证:△AEF是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
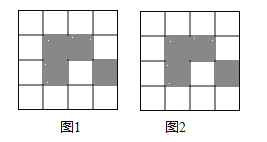
【题目】如图,下列4×4网格图都是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,请在空白小正方形中,按下列要求涂上阴影.
(1)在图1中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个中心对称图形;
(2)在图2中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个轴对称图形,但不是中心对称图形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com