
 如图,在平行四边形ABCD中,AM⊥BC,AN⊥CD,M,N分别为垂足,求证:$\frac{AM}{AB}=\frac{MN}{AC}$.
如图,在平行四边形ABCD中,AM⊥BC,AN⊥CD,M,N分别为垂足,求证:$\frac{AM}{AB}=\frac{MN}{AC}$. 分析 首先根据平行四边形的性质得∠B=∠D,AD=BC,再由AM⊥BC,AN⊥CD得到∠AMB=∠AND=90°,然后根据相似三角形的判定方法可证明△AMB∽△AND,进而得到AM:AN=AB:AD,由于BC=AD,则AM:AN=AB:AC,由AD∥BC得∠DAM=∠AMB=90°,则∠MAN=90°-∠DAN,根据等角的余角相等得到∠MAN=∠D,所以∠B=∠MAN,根据有两组对应边的比相等且夹角相等的两个三角形相似可判断△AMN∽△BAC,然后根据三角形相似的性质即可得到结论.
解答 证明:∵四边形ABCD为平行四边形,
∴∠B=∠D,AD=BC,
∵AM⊥BC,AN⊥CD,
∴∠AMB=∠AND=90°,
∴△AMB∽△AND,
∴AM:AN=AB:AD,
而AD=BC,
∴AM:AN=AB:AC,
即AM:AB=AN:BC①,
∵AD∥BC,
∴∠DAM=∠AMB=90°,
∵∠MAN=90°-∠DAN,
而∠D=90°-∠DAN,
∴∠MAN=∠D,
而∠D=∠B,
∴∠B=∠MAN②,
由①②得△AMN∽△BAC,
∴$\frac{AM}{AB}=\frac{MN}{AC}$.
点评 本题考查了相似三角形的判定与性质:有两组对应边的比相等且夹角相等的两个三角形相似;有两组角对应相等的两三角形相似;相似三角形的对应边的比相等,对应角相等.也考查了平行四边形的性质.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
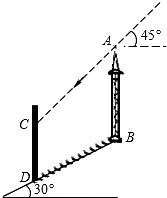 如图,在坡角为30°的山坡上有一铁塔AB,其正前方 矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD的长为4米,落在广告牌上的影子CD的长为3米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号).
如图,在坡角为30°的山坡上有一铁塔AB,其正前方 矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD的长为4米,落在广告牌上的影子CD的长为3米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在菱形ABCD中,过点B作BE⊥AD,BF⊥CD,垂足分别为点E、F,延长BD至点G,使得DG=BD,连结EG、FG,若AE=DE,求tan∠BGE的值.
如图,在菱形ABCD中,过点B作BE⊥AD,BF⊥CD,垂足分别为点E、F,延长BD至点G,使得DG=BD,连结EG、FG,若AE=DE,求tan∠BGE的值.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com