练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    (1)分别以1cm、2cm、3cm为半径作、、，使它们两两外切；

    (2)判断的形状，并说明理由．

    答案：略
    解析：

    (1)作法：①作，使它的半径为1cm；②作=3cm，以为圆心、2cm为半径作圆；③分别以、为圆心，4cm、5cm为半径画弧，两弧相交于点；④以为圆心、3cm为半径作圆．

    (2)因为=3cm，=4cm，=5cm，所以为直角三角形．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，在矩形ABCD中，AB=10cm，BC=20cm．P、Q两点同时从A点出发，分别以1cm/秒和2cm/秒的速度沿A?B?C?D?A运动，当Q点回到A点时，P、Q两点即停止运动，设点P、Q运动时间为t秒．
    （1）当P、Q分别在AB边和BC边上运动时，设以P、B、Q为顶点的三角形面积为s，精英家教网请写出s关于t的函数解析式及自变量t的取值范围；
    （2）在整个运动过程中，t取何值时，PQ与BD垂直？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    18、（不写画法）
    （1）如图△ABC，顶点A（3，7），B（1，3），C（5，2），在直角坐标系中画出△ABC绕着C点顺时针旋转90°得到的△A′B′C′，并写出点B′的坐标．
    （2）分别以1cm，2cm，2cm为半径画圆，使它们两两外切．（要标圆心距的长度）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在△ABC中，∠ACB=90°，∠ABC=30°，BC=6cm，点D、E从点C同时出发，分别以1cm/s和2cm/s的速度沿着射线CB向右移动，以DE为一边在直线BC的上方作等边△DEF，连接CF，设点D、E运动的时间为t秒．
    （1）△DEF的边长为
     
    （用含有t的代数式表示），当t=
     
    秒时，点F落在AB上；
    （2）t为何值时，以点A为圆心，AF为半径的圆与△CDF的边所在的直线相切？
    （3）设点F关于直线AB的对称点为G，在△DEF运动过程中，是否存在某一时刻t，使得以A、C、E、G为顶点的四边形为梯形？若存在，请直接写出t的值；若不存在，请说明理由．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

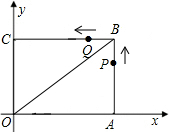    如图，矩形OABC中，AB=10cm，BC=20cm，P、Q两点同时从A点出发，分别以1cm/s和2cm/s的速度沿A→B→C→O→A运动，当Q点到达A点时，P、Q两点立即停止运动，设运动时间为ts．
    （1）当t=7s时，求过O、A、Q三点的抛物线解析式．
    （2）当P、Q分别在AB边和BC边上运动时，为何值时，以Q、B、P三点为顶点的三角形与以C、O、B为顶点的三角形相似？
    （3）设△OPQ的面积为S，试写出S与t的函数关系式及自变量t的范围．
    （4）在整个运动过程中，是否存在PQ⊥BO？若存在，求出直线PQ的解析式；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

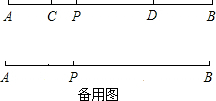    精英家教网如图，P是定长线段AB上一点，C、D两点同时从P、B出发分别以1cm/s和2cm/s的速度沿直线AB向左运动（C在线段AP上，D在线段BP上）．已知C、D运动到任一时刻时，总有PD=2AC．
    （1）线段AP与线段AB的数量关系是：
     
    ；
    （2）若Q是线段AB上一点，且AQ-BQ=PQ，求证：AP=PQ；
    （3）若C、D运动5秒后，恰好有CD=
    1
    2
    AB，此时C点停止运动，D点在线段PB上继续运动，M、N分别是CD、PD的中点，问
    MN
    AB
    的值是否发生变化？若变化，请说明理由；若不变，请求出
    MN
    AB
    的值．

    查看答案和解析>>

    同步练习册答案