
【题目】一个四位数,若首位和末位都是1,称这样的数为“首尾双一数”,例如:1231,1581,1941等都是“首尾双一数”.
(1)证明:一个“首尾双一数”与它去掉首位和末位后得到的两位数的3倍的差能被7整除;
(2)给定一个“首尾双一数”n,记D(n)=![]() ,求满足D(n)是完全平方数,且n的所有位数上的数字之和为偶数的所有n.
,求满足D(n)是完全平方数,且n的所有位数上的数字之和为偶数的所有n.
【答案】(1)见解析;(2)满足条件的n为1221或1971.
【解析】
(1)设出“首尾双一数”,进而表示出它,以及去掉首位和末位得到的两位数,即可得出结论;
(2)设出“首尾双一数”,进而得出D(n)=99+10a+b,再判断出D(n)的范围,利用完全平方数,即可求出n,最后判断即可得出结论.
解:(1)设“首尾双一数”为![]() ,(0<a≤9,0≤b≤9的整数),
,(0<a≤9,0≤b≤9的整数),
则“首尾双一数”为1000+100a+10b+1=1001+100a+10b,
去掉首位和末位后得到的两位数为10a+b,
∴1001+100a+10b﹣3(10a+b)=1001+100a+10b﹣30a﹣3b=1001+70a+7b=7(143+10a+b),
∵0<a≤9,0≤b≤9的整数,
∴143+10a+b为整数,
∴1001+100a+10b﹣3(10a+b)能被7整除,
即:一个“首尾双一数”与它去掉首位和末位后得到的两位数的3倍的差能被7整除;
(2)设一个“首尾双一数”n为![]() ,(0≤a≤9,0≤b≤9的整数),则n=1001+100a+10b,
,(0≤a≤9,0≤b≤9的整数),则n=1001+100a+10b,
∴D(n)=![]() =
=![]() =99+10a+b,
=99+10a+b,
∵0≤a≤9,0≤b≤9的整数),
∴99≤99+10a+b≤198,
∴①99+10a+b=100,
∴10a+b=1,
∴a=0,b=1,
∴n=1011,
而1+0+1+1=3是奇数,不是偶数,不符合题意,
②99+10a+b=121,
∴10a+b=22,
∴a=2,b=2,
∴n=1221,
而1+2+2+1=6是偶数,符合题意,
③99+10a+b=144,
∴10a+b=45,
∴a=4,b=5,
∴n=1451,
而1+4+5+1=11是奇数,不是偶数,不符合题意,
④99+10a+b=169,
∴10a+b=70,
∴a=7,b=0,
∴n=1701,
而1+7+0+1=9是奇数,不是偶数,不符合题意,
⑤99+10a+b=196,
∴10a+b=97,
∴a=9,b=7,
∴n=1971,
而1+9+7+1=318是偶数,符合题意,
即:满足条件的n为1221或1971.


科目:初中数学 来源: 题型:
【题目】小亮一家在一湖泊中游玩,湖泊中有一孤岛,妈妈在孤岛P处观看小亮与爸爸在湖中划船(如图所示).小船从P处出发,沿北偏东60°方向划行200米到A处,接着向正南方向划行一段时间到B处.在B处小亮观测到妈妈所在的P处在北偏西37°的方向上,这时小亮与妈妈相距多少米(精确到1米)?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AB<BC,点E为对角线AC上的一个动点,连接BE,DE,过E作EF⊥BC于F.设AE=x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )
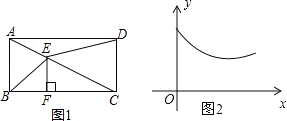
A.线段BEB.线段EFC.线段CED.线段DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,求旗杆AB的高度.
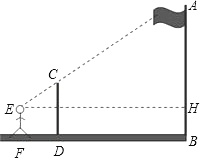
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在黄金矩形ABCD中,四边形ABFG、GHED均为正方形,![]() ,现将矩形ABCD沿AE向上翻折,得四边形AEC'B',连接BB',若AB=2,则线段BB'的长度为( )
,现将矩形ABCD沿AE向上翻折,得四边形AEC'B',连接BB',若AB=2,则线段BB'的长度为( )
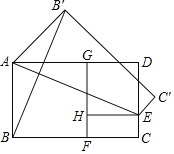
A.![]() B.
B.![]() C.2D.
C.2D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了抓住集安国际枫叶旅游节的商机,某商店决定购进A、B两种旅游纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元;
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C1:y=ax2+bx+c向左平移1个单位长度,再向上平移4个单位长度得到抛物线C2:y=x2.

(1)直接写出抛物线C1的解析式 ;
(2)如图1,已知抛物线C1与x轴交于A,B两点,点A在点B的左侧,点P(![]() ,t)在抛物线C1上,QB⊥PB交抛物线于点Q.求点Q的坐标;
,t)在抛物线C1上,QB⊥PB交抛物线于点Q.求点Q的坐标;
(3)已知点E,M在抛物线C2上,EM∥x轴,点E在点M的左侧,过点M的直线MD与抛物线C2只有一个公共点(MD与y轴不平行),直线DE与抛物线交于另一点N.若线段NE=DE,设点M,N的横坐标分别为m,n,直接写出m和n的数量关系(用含m的式子表示n)为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4月12日华为新出的型号为“P30 Pro”的手机在上海召开发布会,某华为手机专卖网店抓住商机,购进10000台“P30 Pro”手机进行销售,每台的成本是4400元,在线同时向国内、国外发售.第一个星期,国内销售每台售价是5400元,共获利100万元,国外销售也售出相同数量该款手机,但每台成本增加400元,获得的利润却是国内的6倍.
(1)求该店销售该款华为手机第一个星期在国外的售价是多少元?
(2)受中美贸易战影响,第二个星期,国内销售每台该款手机售价在第一个星期的基础上降低m%,销量上涨5m%;国外销售每台售价在第一个星期的基础上上涨m%,并且在第二个星期将剩下的手机全部卖完,结果第二个星期国外的销售总额比国内的销售总额多6993万元,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com