
| A. | -$\frac{5}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{5}{2}$或$\frac{1}{2}$ | D. | 1 |
分析 由根与系数的关系可得:x1+x2=-(m+1),x1•x2=$\frac{1}{2}$,又知一个实数根的倒数恰是它本身,则该实根为1或-1,然后把±1分别代入两根之和的形式中就可以求出m的值.
解答 解:由根与系数的关系可得:
x1+x2=-(m+1),x1•x2=$\frac{1}{2}$,
又知一个实数根的倒数恰是它本身,
则该实根为1或-1,
若是1时,即1+x2=-(m+1),而x2=$\frac{1}{2}$,解得m=-$\frac{5}{2}$;
若是-1时,则m=$\frac{1}{2}$.
故选:C.
点评 本题考查了一元二次方程的解的定义和一元二次方程根与系数的关系.解此类题目要会把代数式变形为两根之积或两根之和的形式,代入数值计算即可.


科目:初中数学 来源: 题型:填空题
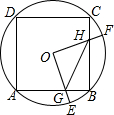 如图,边长为4的正方形ABCD内接于点O,点E是$\widehat{AB}$上的一动点(不与A、B重合),点F是$\widehat{BC}$上的一点,连接OE、OF,分别与AB、BC交于点G,H,且∠EOF=90°,有以下结论:
如图,边长为4的正方形ABCD内接于点O,点E是$\widehat{AB}$上的一动点(不与A、B重合),点F是$\widehat{BC}$上的一点,连接OE、OF,分别与AB、BC交于点G,H,且∠EOF=90°,有以下结论:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
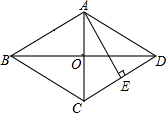 如图,在菱形ABCD中,AC与BD于点O,AE⊥CD,且AE=OD,若AO+OD+AD=3+$\sqrt{3}$,则菱形ABCD的面积是2$\sqrt{3}$.
如图,在菱形ABCD中,AC与BD于点O,AE⊥CD,且AE=OD,若AO+OD+AD=3+$\sqrt{3}$,则菱形ABCD的面积是2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一般情况下,学生注意力上课后逐渐增强,中间有段时间处于较理想的稳定状态,随后开始分散.实验结果表明,学生注意力指数y随时间x(min)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分):
一般情况下,学生注意力上课后逐渐增强,中间有段时间处于较理想的稳定状态,随后开始分散.实验结果表明,学生注意力指数y随时间x(min)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分):查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com