练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】(2016山东省泰安市第22题)如图，半径为3的⊙O与Rt△AOB的斜边AB切于点D，交OB于点C，连接CD交直线OA于点E，若∠B=30°，则线段AE的长为 ．

    【答案】

    【解析】

    试题分析：要求AE的长，只要求出OA和OE的长即可，要求OA的长可以根据∠B=30°和OB的长求得，OE可以根据∠OCE和OC的长求得．连接OD，如图所示，

    由已知可得，∠BOA=90°，OD=OC=3，∠B=30°，∠ODB=90°，∴BO=2OD=6，∠BOD=60°，

    ∴∠ODC=∠OCD=60°，AO=BOtan30°=6×=2，∵∠COE=90°，OC=3，

    ∴OE=OCtan60°=3×=3，∴AE=OE﹣OA=3-2=，

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

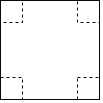
    【题目】如图，把一边长为x厘米的正方形纸板的四个角各剪去一个边长为y厘米的小正方形，然后把它折成一个无盖纸盒．

    （1）该纸盒的高是_____厘米，底面积是_____________平方厘米；

    （2）求该纸盒的全面积（外表面积）；

    （3）为了使纸盒底面更加牢固且达到废物利用的目的，现考虑将剪下的四个小正方形平铺在盒子的底面，要求既不重叠又恰好铺满（不考虑纸板的厚度），求此时x与y之间的倍数关系．（直接写出答案即可）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(2016浙江省舟山市第23题)我们定义：有一组邻角相等的凸四边形叫做“等邻角四边形”

    （1）概念理解：

    请你根据上述定义举一个等邻角四边形的例子；

    （2）问题探究；

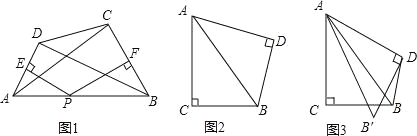
    如图1，在等邻角四边形ABCD中，∠DAB=∠ABC，AD，BC的中垂线恰好交于AB边上一点P，连结AC，BD，试探究AC与BD的数量关系，并说明理由；

    （3）应用拓展；

    如图2，在Rt△ABC与Rt△ABD中，∠C=∠D=90°，BC=BD=3，AB=5，将Rt△ABD绕着点A顺时针旋转角α（0°＜∠α＜∠BAC）得到Rt△AB′D′（如图3），当凸四边形AD′BC为等邻角四边形时，求出它的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在边长为a的正方形的一角减去一个边长为的小正方形（a>b），如图①

    ① ②

    （1）由图①得阴影部分的面积为 .

    （2）沿图①中的虚线剪开拼成图②，则图②中阴影部分的面积为 .

    （3）由（1）（2）的结果得出结论： = .

    （4）利用（3）中得出的结论计算：20172－20162

    查看答案和解析>>

    科目：初中数学 来源： 题型：

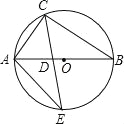
    【题目】(2016山东省泰安市第17题)如图，△ABC内接于⊙O，AB是⊙O的直径，∠B=30°，CE平分∠ACB交⊙O于E，交AB于点D，连接AE，则S△ADE：S△CDB的值等于（ ）

    A．1： B．1： C．1：2 D．2：3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

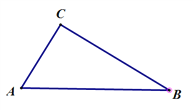
    【题目】（8分）如图，在Rt△ABC中，∠ACB=Rt∠。

    （1）请用直尺和圆规，过点C作AB边上的高线，交AB于D,作∠B的角平分线，交AC于E，交CD与F。

    （2）△CEF是什么三角形，请说明理由

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】近似数2.40×104精确到________位.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

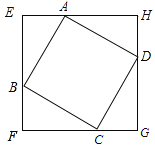
    【题目】如图，正方形ABCD的边长为8cm，分别过四个顶点A、B、C、D做四条直线EF、FG、GH、HE，并保证相邻两条直线垂直，相交于E、F、G、H四点，且AE=BF=CG=DH．

    （1）求证：四边形EFGH是正方形；

    （2）判断无论如何按照上述要求作图，线段EG、AC的中点是否重合，并说明理由；

    （3）判断四边形EFGH的面积有无最大值，若有请写出面积最大值，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数据1460000000用科学记数法表示应是 ．

    查看答案和解析>>

    同步练习册答案