
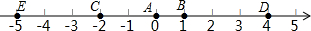 如图,A点的初始位置位于数轴上的原点.现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样.
如图,A点的初始位置位于数轴上的原点.现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样.分析 (1)根据数轴上点的坐标变化和平移规律(左减右加),分别求出点所对应的数,进而求出点到原点的距离;
(2)与(1)同理;
(3)根据前4次移动情况,然后对奇数项、偶数项分别探究,找出其中的规律(相邻两数都相差3),写出表达式就可解决问题.
解答 解:(1)由题意可得:移动1次后该点对应的数为0+1=1,到原点的距离为1,
故答案为:1;
(2)移动2次后该点对应的数为1-3=-2,到原点的距离为2,
故答案为:2;
(3)移动3次后该点对应的数为-2+6=4,到原点的距离为4;
移动4次后该点对应的数为4-9=-5,到原点的距离为5,
∴移动奇数次后该点到原点的距离为$\frac{3n-1}{2}$;
移动偶数次后该点到原点的距离为$\frac{3n-2}{2}$,
当n=2015时,$\frac{3n-1}{2}$=$\frac{2015×3-1}{2}$=3022,
故答案为:3022.
点评 本题考查了数轴,以及用正负数可以表示具有相反意义的量,还考查了数轴上点的坐标变化和平移规律(左减右加),考查了一列数的规律探究.对这列数的奇数项、偶数项分别进行探究是解决这道题的关键.


科目:初中数学 来源: 题型:选择题
| A. | (x+1)(x-1)=x2-1 | B. | a2-b2=(a+b)(a-b) | ||
| C. | x2-2x+1=x(x-2)+1 | D. | mx+my+nx+ny=m(x+y)+n(x+y) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 精确到万分位,有4个有效数字 | B. | 精确到十万分位,有3个有效数字 | ||
| C. | 精确到万分位,有3个有效数字 | D. | 精确到十万分位,有4个有效数字 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC和△ADE都是等边三角形,且点B,A,E在同一直线上,连接BD交AC于M,连接CE交AD于N,连接MN.
如图,△ABC和△ADE都是等边三角形,且点B,A,E在同一直线上,连接BD交AC于M,连接CE交AD于N,连接MN.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在反比例函数y=$\frac{k}{x}$的图象上有一点A,过A作AC垂直x轴于点C,已知点C的坐标为(1,0),点D与点C关于原点对称,且S△ACD=4,直线AD交双曲线的另一支于点B.
如图,在反比例函数y=$\frac{k}{x}$的图象上有一点A,过A作AC垂直x轴于点C,已知点C的坐标为(1,0),点D与点C关于原点对称,且S△ACD=4,直线AD交双曲线的另一支于点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2a<-2b | B. | a+m>b+m | C. | am>bm | D. | $\frac{a}{3}$>$\frac{b}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com