
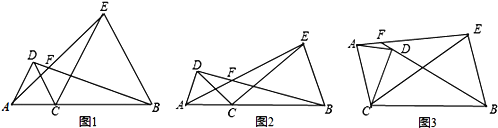
����Ŀ����֪��CΪ�߶�AB��һ�㣬�ֱ���AC��BCΪ�����߶�ABͬ������ACD�͡�BCE����CA=CD��CB=CE����ACD=��BCE��ֱ��AE��BD���ڵ�F
��1����ͼ1������ACD=60�b�����AFB= ��
��2����ͼ2������ACD=�������AFB= ���ú�����ʽ�ӱ�ʾ����
��3����ͼ2�еġ�ACD�Ƶ�C˳ʱ����ת����Ƕȣ�����F������BD��AE�е�һ���߶��ϣ�����ͼ3����̽����AFB�����������ϵ��������֤����
���𰸡�(1)120��;(2) 180��D��;(3)������
�������������������1�������ACE=��DCB��֤��ACE�ա�DCB���Ƴ���CAE=��CDB�������AFB=��CDA+��DAC�������������ڽǺͶ���������ɣ�
��2�������ACE=��DCB��֤��ACE�ա�DCB���Ƴ���CAE=��CDB�������AFB=��CDA+��DAC�������������ڽǺͶ������������
��3�������ACE=��DCB��֤��ACE�ա�DCB���Ƴ���CAE=��CDB�������AFB=��CEB+��CBE�������������ڽǺͶ������������
����������⣺��1���ߡ�ACD=��BCE�����ACD+��DCE=��BCE+��DCE�����ACE=��DCB������ACE����DCB��

����ACE����DCB�����CAE=��CDB�����AFB=��CDB+��CDA+��DAE
=��CDA+��DAE+��BAE
=��CDA+��DAC
=180��D60��
=120����
��2���⣺�ߡ�ACD=��BCE�����ACD+��DCE=��BCE+��DCE�����ACE=��DCB������ACE����DCB��
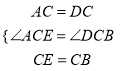
����ACE����DCB�����CAE=��CDB�����AFB=��CDB+��CDA+��DAE
=��CDA+��DAE+��BAE
=��CDA+��DAC
=180��D��ACD
=180��D����
��3����AFB=180-����֤�����ߡ�ACD=��BCE�����ACD+��DCE=��BCE+��DCE�����ACE=��DCB������ACE����DCB��
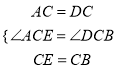
����ACE����DCB�����AEC=��DBC�����AFB=��AEC+��CEB+��EBD
=��DBC+��CEB+��EBC
=��CEB+��EBC
=180��-��ECB
=180��-����


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
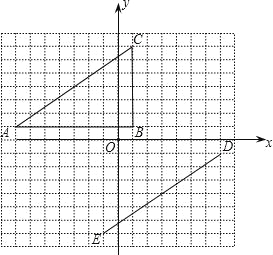
����Ŀ����ƽ��ֱ������ϵ�У���ABC�Ķ���������A����7��1����B��1��1����C��1��7�����߶�DE�Ķ˵�������D��7����1����E����1����7����
��1����˵�����ƽ���߶�AC��ʹ�����߶�ED�غϣ�
��2������ABC������ԭ��O��ʱ����ת��ʹAC�Ķ�Ӧ��ΪDE����ֱ��д����B�Ķ�Ӧ��F�����ꣻ
��3��������2���е���DEF��������ABCͬʱ������ԭ��O��ʱ����ת90�㣬������ת���ͼ�Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����P��Q����ֱ��l��ĵ㣬����˵����ȷ���ǣ�������
A.����PQ����PQһ����ֱ��l��ֱ
B.����PQ����PQһ����ֱ��lƽ��
C.����PQ����PQһ����ֱ��l�ཻ
D.����Pֻ�ܻ�һ��ֱ����ֱ��lƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�������̶�����һ��ǽ��ǽ�ij��Ȳ��ޣ�����40�׳������Χ��һ�������εIJֿ⣮
��1�����ε������150ƽ���ף�������������ڱߵij���
��2���ܷ�Χ�����220ƽ���ij����Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������IJ���Ϊ29��18�䣬������Ĵ�СΪ��������
A. 150��42�� B. 60��42�� C. 150��82�� D. 60��82��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��������һ�������÷����������������ϵ�ש������ṹ��ͼ��ʾ������ͼ�е����ݣ���λ��m��������������⣺ 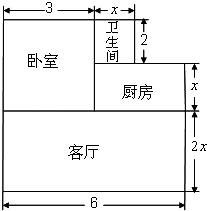
��1���ú�x��ʽ�ӱ�ʾ���������m2 �� ���ҵ����m2 ��
��2���˾������÷��������Ϊm2 ��
��3����֪��������������������2m2 �� ����1m2��ש��ƽ������Ϊ80Ԫ����ô�̵�ש���ܷ���Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����������У�ij�˶�Աǰ7���������62���������Ҫ����89����10��������ļ�¼����ô��8�����������Ҫ���______���ijɼ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ��ش����⣺
����
��1������ijʮ��·�ڵ�����������ֱ�У�Ҳ��������ת������ת����������ֿ����ԵĴ�С��ͬ�������������������ʮ��·��ʱ������Ҫ����������ת�ĸ���
��2�������Ѳ�ͬ����������Կ�ף���������Կ�ֱ��ܴ�����������һ��Կ��ֻ�ܿ�һ��������������Կ�ײ��ܴ��������������ȡ��һ��Կ������һ������һ�δ����ĸ����Ƕ��٣�
���ǿ����á���������������ģ����1���ڿڴ��з�������ͬ��ɫ��С�����ʾֱ�У������ʾ����ת�������ʾ����ת��������������·�ڣ��൱�ڴ����������Ŀڴ��и��������һ��.
���⣺
��1���¼�������������������ת���൱�ڡ��������������е�ʲô�¼���
��2�����һ����������������ģ����2�����Ҫ˵����ķ���
��3����ֱ��д����2�Ľ����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com