练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图所示，抛物线的顶点为A，直线：与 轴的交点为B，其中.

    ⑴　写出抛物线对称轴及顶点A的坐标（用含的代数式表示）；

    ⑵　证明点A在直线上，并求出的度数；

    ⑶　动点Q在抛物线对称轴上，问抛物线上是否存在点P，使以P、Q、A为顶点的三角形与全等？若存在，求出的值，并写出所有符合上述条件的P点坐标；若不存在，说明理由.
    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

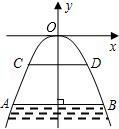    精英家教网如图所示，有一座抛物线形拱桥，桥下面在正常水位AB时，宽20m，水位上升3m就达到警戒线CD，这时水面宽度为10m．
    （1）在如图的坐标系中求抛物线的解析式；
    （2）若洪水到来时，水位以每小时0.2m的速度上升，从警戒线开始，再持续多少小时才能到达拱桥顶？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

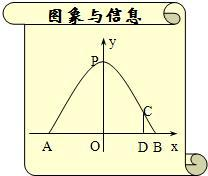    如图所示，已知：一抛物线形拱门，其地面宽度AB=18m，小明站在门内，在离门脚B点1m远的点D处精英家教网，垂直地面立起一根1.7m长的木杆，其顶端恰好顶在抛物线形门上C处，建立如图所示的坐标系．
    （1）求出拱门所在抛物线的解析式；
    （2）求出该大门的高度OP．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，某隧道的截面是由一抛物线和一矩形构成，其行车道CD总宽度为8米，隧道为单行线2车道．
    （1）以矩形一边EF所在直线为x轴，经过隧道顶端最高点H且垂直于EF的直线为y轴，建立如图所示的平面直角坐标系，求出此抛物线的解析式；
    （2）在隧道拱的两侧距地面3米高处各安装一盏路灯，在（1）的平面直角坐标系中，用坐标表示其中一盏路灯的位置；
    （3）为了保证行车安全，要求行驶车辆顶部（设为平顶）与隧道拱在竖直方向上高度之差至少有0.5米．现有一辆汽车，装载货物后，其宽度为4米，车载货物的顶部与路面的距离为2.5米，该车能否通过这个隧道？请说明理由．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图所示，有一座抛物线形拱桥，桥下面在正常水位时，AB宽20m，水位上升到警戒线CD时，CD到拱桥顶E的距离仅为1m，这时水面宽度为10m．
    （1）在如图所示的坐标系中求抛物线的解析式；
    （2）若洪水到来时，水位以每小时0.3m的速度上升，从正常水位开始，持续多少小时到达警戒线？

    查看答案和解析>>

    科目：初中数学 来源：江苏期末题 题型：解答题

    如图，有一座抛物线形拱桥，在正常水位时水面AB的宽为20米，此时拱桥的顶端点O距离水面4米。
    （1）建立如图所示的直角坐标系，利用待定系数法求出此抛物线的解析式；
    （2）当水位在正常水位时，有一只宽为8米的货船经过该桥，船上装有高出水面3.5米的长方体货物（货物与货船同宽），问：此船能否安全通过这座拱桥？

    查看答案和解析>>

    同步练习册答案