
 a.
a. -1)a,BC:AC=(
-1)a,BC:AC=(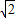 -1)a:
-1)a: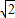 a=1:(2+
a=1:(2+ )
)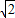 ):2.(8分)
):2.(8分)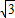 -
-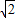 +1):
+1):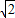 或(
或( +
+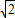 -2):2.
-2):2.

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
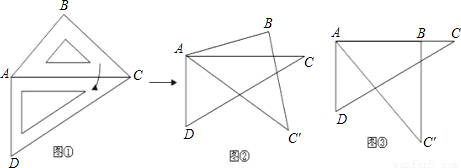
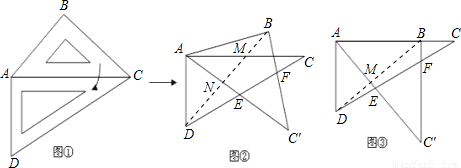
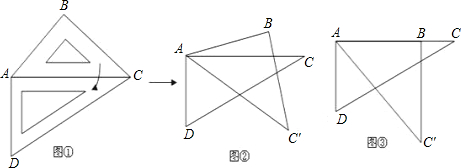
 22、取一副三角板按图1拼接,固定三角板ADC,将三角板ABC绕点A依顺时针方向旋转一个大小为α的角(0°<α≤45°)得到△ABC′,如图所示.
22、取一副三角板按图1拼接,固定三角板ADC,将三角板ABC绕点A依顺时针方向旋转一个大小为α的角(0°<α≤45°)得到△ABC′,如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:044
(2006安徽,23)(13分)取一副三角板按图①拼接,固定三角板ADC,将三板ABC绕点A依顺时针方向旋转一个大小为α的角(0°<α≤45°)得到△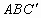 ,如图所示.
,如图所示.
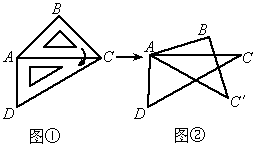
试问:(1)当α为多少度时,能使得图②中AB∥DC?
(2)当旋转到图③位置,此时α又为多少度?图③中你能找出哪几对相似三角形,并求其中一对的相似比;

图③
(3)连结BD,当0°<α≤45°时,探寻∠ 值的大小变化情况,并给出你的证明.
值的大小变化情况,并给出你的证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
取一副三角板按图①拼接,固定三角板ADC,将三角板ABC绕点A依顺时针方向旋转一个大小为α的角(0°<α≤45°得到⊿ABC/,如图②所示。试问:
1.当α为多少度时,能使得图②中AB∥CD?
2.当旋转至图③位置,此时α又为多少度?图③中你能找出哪几对相似三角形,并求其中一对的相似比。
3.连结BD,当0°<α≤45°时,探寻∠DBC/+∠CAC/+∠BDC值的大小变化情况,并给出你的证明。
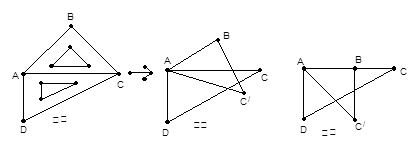
查看答案和解析>>
科目:初中数学 来源:2013届江苏苏州星港学校八年级下5月月考数学试卷(解析版) 题型:解答题
取一副三角板按图①拼接,固定三角板ADC,将三角板ABC绕点A依顺时针方向旋转一个大小为α的角(0°<α≤45°得到⊿ABC/,如图②所示。试问:
1.当α为多少度时,能使得图②中AB∥CD?
2.当旋转至图③位置,此时α又为多少度?图③中你能找出哪几对相似三角形,并求其中一对的相似比。
3.连结BD,当0°<α≤45°时,探寻∠DBC/+∠CAC/+∠BDC值的大小变化情况,并给出你的证明。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com