
【题目】问题提出
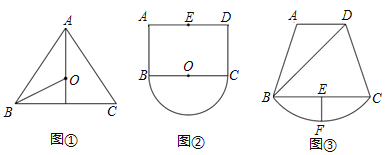
(1)如图①,在△ABC中,AB=AC=10,BC=12,点O是△ABC的外接圆的圆心,则OB的长为
问题探究
(2)如图②,已知矩形ABCD,AB=4,AD=6,点E为AD的中点,以BC为直径作半圆O,点P为半圆O上一动点,求E、P之间的最大距离;
问题解决
(3)某地有一块如图③所示的果园,果园是由四边形ABCD和弦CB与其所对的劣弧场地组成的,果园主人现要从入口D到![]() 上的一点P修建一条笔直的小路DP.已知AD∥BC,∠ADB=45°,BD=120
上的一点P修建一条笔直的小路DP.已知AD∥BC,∠ADB=45°,BD=120![]() 米,BC=160米,过弦BC的中点E作EF⊥BC交
米,BC=160米,过弦BC的中点E作EF⊥BC交![]() 于点F,又测得EF=40米.修建小路平均每米需要40元(小路宽度不计),不考虑其他因素,请你根据以上信息,帮助果园主人计算修建这条小路最多要花费多少元?
于点F,又测得EF=40米.修建小路平均每米需要40元(小路宽度不计),不考虑其他因素,请你根据以上信息,帮助果园主人计算修建这条小路最多要花费多少元?
【答案】(1)![]() ;(2)E、P之间的最大距离为7;(3)修建这条小路最多要花费
;(2)E、P之间的最大距离为7;(3)修建这条小路最多要花费![]() 元.
元.
【解析】
(1)若AO交BC于K,则AK=8,在Rt△BOK中,设OB=x,可得x2=62+(8﹣x)2,解方程可得OB的长;
(2)延长EO交半圆于点P,可求出此时E、P之间的最大距离为OE+OP的长即可;
(3)先求出![]() 所在圆的半径,过点D作DG⊥BC,垂足为G,连接DO并延长交
所在圆的半径,过点D作DG⊥BC,垂足为G,连接DO并延长交![]() 于点P,则DP为入口D到
于点P,则DP为入口D到![]() 上一点P的最大距离,求出DP长即可求出修建这条小路花费的最多费用.
上一点P的最大距离,求出DP长即可求出修建这条小路花费的最多费用.
(1)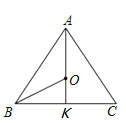
如图,若AO交BC于K,
∵点O是△ABC的外接圆的圆心,AB=AC,
∴AK⊥BC,BK=![]() ,
,
∴AK=![]() ,
,
在Rt△BOK中,OB2=BK2+OK2,设OB=x,
∴x2=62+(8x)2,
解得x=![]() ,
,
∴OB=![]() ;
;
故答案为:![]() .
.
(2)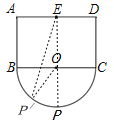
如图,连接EO,延长EO交半圆于点P,可求出此时E、P之间的距离最大,
∵在![]() 是任意取一点异于点P的P′,连接OP′,P′E,
是任意取一点异于点P的P′,连接OP′,P′E,
∴EP=EO+OP=EO+OP′>EP′,即EP>EP′,
∵AB=4,AD=6,
∴EO=4,OP=OC=![]() ,
,
∴EP=OE+OP=7,
∴E、P之间的最大距离为7.
(3)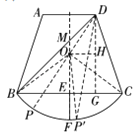
作射线FE交BD于点M,
∵BE=C,EF⊥BC,![]() 是劣弧,
是劣弧,
∴![]() 所在圆的圆心在射线FE上,
所在圆的圆心在射线FE上,
假设圆心为O,半径为r,连接OC,则OC=r,OE=r40,BE=CE=![]() ,
,
在Rt△OEC中,r2=802+(r40)2,
解得:r=100,
∴OE=OFEF=60,
过点D作DG⊥BC,垂足为G,
∵AD∥BC,∠ADB=45°,
∴∠DBC=45°,
在Rt△BDG中,DG=BG=![]() ,
,
在Rt△BEM中,ME=BE=80,
∴ME>OE,
∴点O在△BDC内部,
∴连接DO并延长交![]() 于点P,则DP为入口D到
于点P,则DP为入口D到![]() 上一点P的最大距离,
上一点P的最大距离,
∵在![]() 上任取一点异于点P的点P′,连接OP′,P′D,
上任取一点异于点P的点P′,连接OP′,P′D,
∴DP=OD+OP=OD+OP′>DP′,即DP>DP′,
过点O作OH⊥DG,垂足为H,则OH=EG=40,DH=DGHG=DGOE=60,
∴![]() ,
,
∴DP=OD+r=![]() ,
,
∴修建这条小路最多要花费40×![]() 元.
元.


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的外接圆,连结OA、OB、OC,延长BO与AC交于点D,与
的外接圆,连结OA、OB、OC,延长BO与AC交于点D,与![]() 交于点F,延长BA到点G,使得
交于点F,延长BA到点G,使得![]() ,连接FG.
,连接FG.
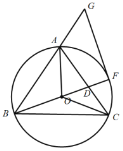

备用图
(1)求证:FG是![]() 的切线;
的切线;
(2)若![]() 的半径为4.
的半径为4.
①当![]() ,求AD的长度;
,求AD的长度;
②当![]() 是直角三角形时,求
是直角三角形时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
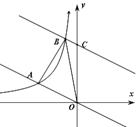
【题目】如图,在平面直角坐标系中,直线![]() 与反比例函数
与反比例函数![]()
![]() 在第二象限内的图象相交于点
在第二象限内的图象相交于点![]() ,将直线
,将直线![]() 向上平移后与反比例函数图象在第二象限内交于点
向上平移后与反比例函数图象在第二象限内交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且
,且![]() 的面积为3,则直线
的面积为3,则直线![]() 的关系式为:________
的关系式为:________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为
的边长为![]() ,
,![]() 在正方形外,
在正方形外,![]() ,过
,过![]() 作
作![]() 于
于![]() ,直线
,直线![]() ,
,![]() 交于点
交于点![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() ,则下列结论正确的是( )
,则下列结论正确的是( )

①![]() ;②
;②![]() ;③
;③![]() ;
;
④若![]() ,则
,则![]()
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() .动点
.动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒
以每秒![]() 个单位长度的速度向终点
个单位长度的速度向终点![]() 运动,当点
运动,当点![]() 与点
与点![]() 、
、![]() 不重合时,过点
不重合时,过点![]() 作
作![]() 交折线
交折线![]() 于点
于点![]() ,以
,以![]() 为边向左作正方形
为边向左作正方形![]() .设正方形
.设正方形![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() (平方单位),点
(平方单位),点![]() 运动的时间为
运动的时间为![]() (秒).
(秒).
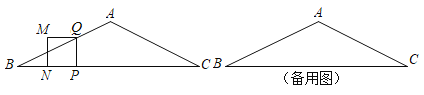
备用图
(1)用含![]() 的代数式表示
的代数式表示![]() 的长.
的长.
(2)直接写出点![]() 在
在![]() 内部时
内部时![]() 的取值范围.
的取值范围.
(3)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(4)直接写出点![]() 落在
落在![]() 的中位线所在直线上时
的中位线所在直线上时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() ,
,![]() 在二次函数
在二次函数![]() 的图象上,点
的图象上,点![]() 是函数图象的顶点,则( )
是函数图象的顶点,则( )
A.当![]() 时,
时,![]() 的取值范围是
的取值范围是![]()
B.当![]() 时,
时,![]() 的取值范围是
的取值范围是![]()
C.当![]() 时,
时,![]() 的取值范围是
的取值范围是![]()
D.当![]() 时,
时,![]() 的取值范围是
的取值范围是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】诗词是我国古代文化中的瑰宝,某市教育主管部门为了解本市初中生对诗词的学习情况;举了一次“中华诗词”背诵大赛,随机抽取了部分同学的成绒(![]() 为整数,总分100分),绘制了如下尚不完整的统计图表.
为整数,总分100分),绘制了如下尚不完整的统计图表.
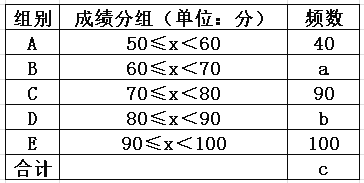

根据以上信息解答下列问题:
(1)统计表中![]() ________,
________,![]() ________,
________,![]() ________;
________;
(2)扇形统计图中,![]() 的值为________,“
的值为________,“![]() ”所对应的圆心角的度数是________(度);
”所对应的圆心角的度数是________(度);
(3)若参加本次大赛的同学共有4000人,请你估计成绩在80分及以上的学生大约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com