
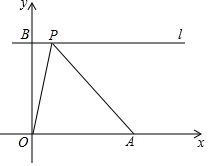
 如图,在平面直角坐标系中,点A的坐标为(5,0),点B的坐标为(0,4),过点B作直线l平行x轴,点P在直线l上运动.设点P的横坐标为a,记点B关于直线OP的对称点为B′,若点B′落在△OAP内部(不包括边上),则a的取值范围为2<a<4.
如图,在平面直角坐标系中,点A的坐标为(5,0),点B的坐标为(0,4),过点B作直线l平行x轴,点P在直线l上运动.设点P的横坐标为a,记点B关于直线OP的对称点为B′,若点B′落在△OAP内部(不包括边上),则a的取值范围为2<a<4. 分析 根据点P在直线l上运动,从左到右依次画图讨论,发现分五种情况::①当点P在点B的左侧运动时,如图1,②当点P与B重合时,点B′也与B重合,此时B′在△OAP的边上,③当点P继续从B点向右运动时,如图2,点B关于直线OP的对称点为B′在△OAP外部,通过画图得这三种情况不符合题意;
④当点B关于直线OP的对称点为B′在△OAP的边AP上时,如图3,作辅助线计算a=2,虽然此种情况不符合条件,但从这一点开始继续向右运动,点B′在△OAP内部,一直到第⑤种情况为止,都满足条件,由此可得
a的取值范围.
解答 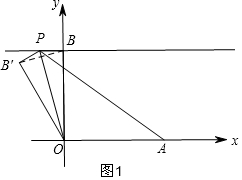 解:①当点P在点B的左侧运动时,如图1,点B关于直线OP的对称点为B′在△OAP外部,此种情况不符合题意;
解:①当点P在点B的左侧运动时,如图1,点B关于直线OP的对称点为B′在△OAP外部,此种情况不符合题意;
②当点P与B重合时,点B′也与B重合,此时B′在△OAP的边上,此种情况不符合题意;
③当点P继续从B点向右运动时,如图2,点B关于直线OP的对称点为B′在△OAP外部,此种情况不符合题意;
④当点B关于直线OP的对称点为B′在△OAP的边AP上时,
如图3,过A作AC⊥PB于C,
此时,PB=a,OB=4,OA=5,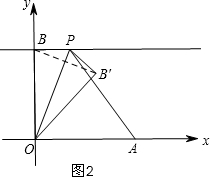
则AC=OB=4,PC=5-a,
∵点B关于直线OP的对称点为B′,
∴OP是BB′的垂直平分线,
∴PB=PB′=a,OB=OB′=4,
∵OP=OP,
∴△BOP≌△B′OP,
∴∠OB′P=∠OBP=90°,
在Rt△AOB′中,AB′=$\sqrt{O{A}^{2}-OB{′}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
由勾股定理得:42+(5-a)2=(a+3)2,
a=2;
⑤当PB=4时,△OBP为等腰直角三角形,点B关于直线OP的对称点为B′在OA上,如图4,
此时a=4,
综上所述,a的取值范围为:2<a<4;
故答案为:2<a<4.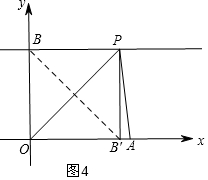
点评 本题是动点与轴对称变换问题,考查了轴对称的性质和坐标与图形的变化,明确轴对称的对应点连线被对称轴垂直平分,正确根据点的坐标写出线段的长,本题利用数形结合的思想解决问题,使答案更为准确.


科目:初中数学 来源: 题型:填空题
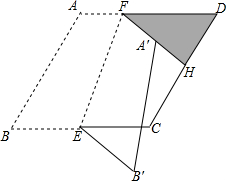 已知菱形ABCD,AB=2,∠ABC=60°,E为BC的中点,点F为边AD上一点,以EF为折痕将四边形ABEF折叠得到四边形A′B′EF.
已知菱形ABCD,AB=2,∠ABC=60°,E为BC的中点,点F为边AD上一点,以EF为折痕将四边形ABEF折叠得到四边形A′B′EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com