
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨÷±œþ![]() ”Î
”Î![]() ÷·Ωª”⁄µ„
÷·Ωª”⁄µ„![]() £¨”Î
£¨”Î![]() ÷·Ωª”⁄µ„
÷·Ωª”⁄µ„![]() £¨≈◊ŒÔœþ
£¨≈◊ŒÔœþ![]() æ≠π˝µ„
æ≠π˝µ„![]() ∫Õµ„
∫Õµ„![]() £¨”Î
£¨”Î![]() ÷·Ωª”⁄¡Ì“ªµ„
÷·Ωª”⁄¡Ì“ªµ„![]() £Æ
£Æ
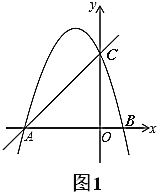
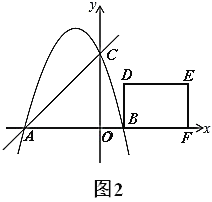
£®1£©«Û≈◊ŒÔœþ±Ì¥Ô Ω£ª
£®2£©‘⁄µ⁄∂˛œÛœÞµƒ≈◊ŒÔœþ…œ”–“ªµ„![]() £¨«“µ„
£¨«“µ„![]() µΩœþ∂Œ
µΩœþ∂Œ![]() µƒæý¿ÎŒ™
µƒæý¿ÎŒ™![]() £¨«Ûµ„
£¨«Ûµ„![]() µƒ◊¯±Í£ª
µƒ◊¯±Í£ª
£®3£©æÿ–Œ![]() µƒ±þ
µƒ±þ![]() ‘⁄
‘⁄![]() ÷·µƒ’˝∞Î÷·£¨
÷·µƒ’˝∞Î÷·£¨![]() ‘⁄µ⁄“ªœÛœÞ£¨
‘⁄µ⁄“ªœÛœÞ£¨![]() £¨
£¨![]() £¨Ω´æÿ–Œ
£¨Ω´æÿ–Œ![]() —ÿ
—ÿ![]() ÷·∏∫∑ΩœÚ∆Ω“∆
÷·∏∫∑ΩœÚ∆Ω“∆![]()
![]() £¨÷±œþ
£¨÷±œþ![]() °¢
°¢![]() ∑÷±Ωª≈◊ŒÔœþ”⁄
∑÷±Ωª≈◊ŒÔœþ”⁄![]() °¢
°¢![]() £ÆŒ £∫ «∑ҥʑ⁄ µ ˝
£ÆŒ £∫ «∑ҥʑ⁄ µ ˝![]() £¨ πµ√“‘µ„
£¨ πµ√“‘µ„![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() Œ™∂•µ„µƒÀƒ±þ–Œ «∆Ω––Àƒ±þ–Œ£ø»Ù¥Ê‘⁄£¨«Î÷±Ω”–¥≥ˆ
Œ™∂•µ„µƒÀƒ±þ–Œ «∆Ω––Àƒ±þ–Œ£ø»Ù¥Ê‘⁄£¨«Î÷±Ω”–¥≥ˆ![]() µƒ÷µ£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
µƒ÷µ£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
°æ¥∞∏°ø£®1£©![]() £ª£®2£©Pµ„◊¯±ÍŒ™£®-1,4£©ªÚ£®-2,3£©£ª£®3£©t=
£ª£®2£©Pµ„◊¯±ÍŒ™£®-1,4£©ªÚ£®-2,3£©£ª£®3£©t=![]() £ª
£ª
°æΩ‚Œˆ°ø
£®1£©¥˝∂®œµ ˝∑®º¥ø…«Ûµ√≈◊ŒÔœþ∑Ω≥ãª
£®2£©◊˜PD°Õx÷·Ωª÷±œþ![]() ”⁄µ„D£¨ΩªAC”⁄µ„E£¨¡¨Ω”PA£¨PC£¨…ËP£®t£¨-t-2t+3£©£¨”…»˝Ω«–Œ√ʪ˝π´ Ωø…µ√S°˜PAC=S°˜PEA+S°˜PEC=
”⁄µ„D£¨ΩªAC”⁄µ„E£¨¡¨Ω”PA£¨PC£¨…ËP£®t£¨-t-2t+3£©£¨”…»˝Ω«–Œ√ʪ˝π´ Ωø…µ√S°˜PAC=S°˜PEA+S°˜PEC=![]() +
+![]() =
=![]() =
=![]() t-
t-![]() t=
t=![]() =
=![]() ,À˘“‘
,À˘“‘![]() t-
t-![]() t=3£¨Ω‚µ√∑Ω≥ú¥Œ™Pµ„∫·◊¯±Í£¨º¥ø…«Ûµ√£ª
t=3£¨Ω‚µ√∑Ω≥ú¥Œ™Pµ„∫·◊¯±Í£¨º¥ø…«Ûµ√£ª
£®3£©ºŸ…˥ʑ⁄t£¨»Áœ¬Õº£¨∏˘æð∫Ø ˝◊¯±Í¡–≥ˆDG£¨FHµƒ÷µ£¨¡ÓDG=FH£¨Ω‚µ√tº¥ø….
£®1£©‘⁄![]() ÷–£¨¡Ó
÷–£¨¡Ó![]() £¨‘Ú
£¨‘Ú![]() £ª
£ª
¡Ó![]() £¨‘Ú
£¨‘Ú![]() £ª
£ª
°ý![]() £¨
£¨![]()
°þ≈◊ŒÔœþ![]() æ≠π˝
æ≠π˝![]() °¢
°¢![]() ¡Ωµ„£¨
¡Ωµ„£¨
°ý![]() £¨
£¨
°ý![]() £¨
£¨
°ý≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™![]() £¨
£¨
£®2£©»ÁÕº£¨
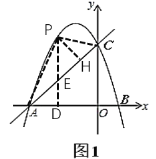
◊˜PD°Õx÷·Ωª÷±œþ![]() ”⁄µ„D£¨ΩªAC”⁄µ„E£¨¡¨Ω”PA£¨PC£¨
”⁄µ„D£¨ΩªAC”⁄µ„E£¨¡¨Ω”PA£¨PC£¨
…ËP£®t£¨-t-2t+3£©£¨
‘ÚDµ„◊¯±ÍŒ™£®t£¨0£©£¨E£®t£¨t+3£©£¨
°ýPE=PD-DE=-t-2t+3-t-3=-t-3t£¨
°ýS°˜PAC=S°˜PEA+S°˜PEC=![]() +
+![]()
=![]() =
=![]()
=![]() (-t-3t)°¡3=
(-t-3t)°¡3=![]() t-
t-![]() t£¨
t£¨
”÷°þS°˜PAC=![]() =
=![]() =3,
=3,
°ý![]() t-
t-![]() t=3£¨Ω‚µ√t=-1ªÚt=-2£¨
t=3£¨Ω‚µ√t=-1ªÚt=-2£¨
°ýPµ„◊¯±ÍŒ™£®-1,4£©ªÚ£®-2,3£©£ª
£®3£©ºŸ…˥ʑ⁄ µ ˝![]() £¨ πµ√“‘µ„
£¨ πµ√“‘µ„![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() Œ™∂•µ„µƒÀƒ±þ–Œ «∆Ω––Àƒ±þ–Œ£¨»ÁÕºÀ˘ 棨Bµ„∆Ω“∆µΩMµ„Œª÷√£¨
Œ™∂•µ„µƒÀƒ±þ–Œ «∆Ω––Àƒ±þ–Œ£¨»ÁÕºÀ˘ 棨Bµ„∆Ω“∆µΩMµ„Œª÷√£¨
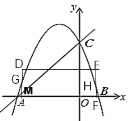
°ýMµ„◊¯±ÍŒ™£®1-t£¨0£©£¨D£®1-t£¨2£©£¨G£®1-t£¨-t+4t£©£¨
°ýDG=-t-4t+2£¨
Õ¨¿Ì£¨F£®4-t£¨0£©£¨H£®4-t£¨-t+10t-21£©£¨
°ýHF=-t+10t-21£¨
°þÀƒ±þ–ŒDGFH «∆Ω––Àƒ±þ–Œ£¨DG°ŒFH£¨
°ýDG=FH£¨
°ý-t-4t+2=-t+10t-21£¨Ω‚µ√t=![]() £¨
£¨
°ý¥Ê‘⁄ µ ˝![]() =
=![]() £¨ πµ√“‘µ„
£¨ πµ√“‘µ„![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() Œ™∂•µ„µƒÀƒ±þ–Œ «∆Ω––Àƒ±þ–Œ.
Œ™∂•µ„µƒÀƒ±þ–Œ «∆Ω––Àƒ±þ–Œ.


 ÷–øº¿˚Ω£÷–øº ‘æ̪„±ýœµ¡–¥∞∏
÷–øº¿˚Ω£÷–øº ‘æ̪„±ýœµ¡–¥∞∏ ΩÔ˝ ¿º“◊¥‘™æÌœµ¡–¥∞∏
ΩÔ˝ ¿º“◊¥‘™æÌœµ¡–¥∞∏ ª∆∏‘øŒÃ√◊˜“µ±æœµ¡–¥∞∏
ª∆∏‘øŒÃ√◊˜“µ±æœµ¡–¥∞∏ µ•‘™º”∆⁄ƒ©∏¥œ∞œ»∑Ê¥ÛøºæÌœµ¡–¥∞∏
µ•‘™º”∆⁄ƒ©∏¥œ∞œ»∑Ê¥ÛøºæÌœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
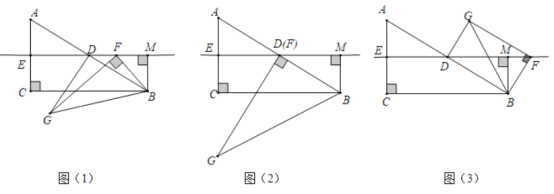
°æƒø°ø»ÁÕº£®1£©£¨‘⁄![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨µ„
£¨µ„![]() ∑÷± «
∑÷± «![]() µƒ÷–µ„£¨π˝µ„
µƒ÷–µ„£¨π˝µ„![]() ◊˜÷±œþ
◊˜÷±œþ![]() µƒ¥πœþ∂Œ
µƒ¥πœþ∂Œ![]() ¥π◊„Œ™
¥π◊„Œ™![]() £Æµ„
£Æµ„![]() «÷±œþ
«÷±œþ![]() …œ“ª∂ص„£¨◊˜
…œ“ª∂ص„£¨◊˜![]() π
π![]() £¨
£¨![]() ¡¨Ω”
¡¨Ω”![]() £Æ
£Æ
£®1£©π€≤Ï≤¬œÎ£∫»ÁÕº£®2£©£¨µ±µ„![]() ”ε„
”ε„![]() ÷ÿ∫œ ±£¨‘Ú
÷ÿ∫œ ±£¨‘Ú![]() µƒ÷µŒ™ £Æ
µƒ÷µŒ™ £Æ
£®2£©Œ ÂÃΩæø£∫»ÁÕº£®1£©£¨µ±µ„![]() ”ε„
”ε„![]() ≤ª÷ÿ∫œ ±£¨«Î«Û≥ˆ
≤ª÷ÿ∫œ ±£¨«Î«Û≥ˆ![]() µƒ÷µº∞¡Ω÷±œþ
µƒ÷µº∞¡Ω÷±œþ![]() º–Ω«»ÒΩ«µƒ∂» ˝£¨≤¢Àµ√˜¿Ì”…
º–Ω«»ÒΩ«µƒ∂» ˝£¨≤¢Àµ√˜¿Ì”…
£®3£©Œ Ã‚Ω‚æˆ£∫»ÁÕº£®3£©£¨µ±µ„![]() ‘⁄Õ¨“ª÷±œþ…œ ±£¨«Î÷±Ω”–¥≥ˆ
‘⁄Õ¨“ª÷±œþ…œ ±£¨«Î÷±Ω”–¥≥ˆ![]() µƒ÷µ£Æ
µƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™£∫’˝∑Ω–Œ![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() »∆µ„
»∆µ„![]() À≥ ±’Ζ˝◊™£¨À¸µƒ¡Ω±þ∑÷±Ωª
À≥ ±’Ζ˝◊™£¨À¸µƒ¡Ω±þ∑÷±Ωª![]() £®ªÚÀ¸√«µƒ—”≥§œþ£©”⁄µ„
£®ªÚÀ¸√«µƒ—”≥§œþ£©”⁄µ„![]() £Æ
£Æ
µ±![]() »∆µ„
»∆µ„![]() –˝◊™µΩ
–˝◊™µΩ![]() ±£®»ÁÕº1£©£¨“◊÷§
±£®»ÁÕº1£©£¨“◊÷§![]() £Æ
£Æ
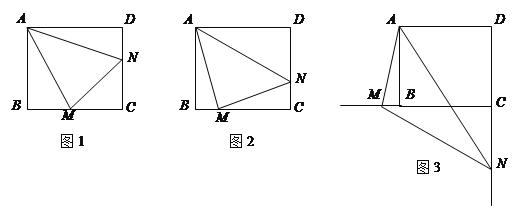
£®1£©µ±![]() »∆µ„
»∆µ„![]() –˝◊™µΩ
–˝◊™µΩ![]() ±£®»ÁÕº2£©£¨œþ∂Œ
±£®»ÁÕº2£©£¨œþ∂Œ![]() ∫Õ
∫Õ![]() ÷ƺ‰”–‘ı—˘µƒ ˝¡øπÿœµ£ø–¥≥ˆ≤¬œÎ£¨≤¢º”“‘÷§√˜£Æ
÷ƺ‰”–‘ı—˘µƒ ˝¡øπÿœµ£ø–¥≥ˆ≤¬œÎ£¨≤¢º”“‘÷§√˜£Æ
£®2£©µ±![]() »∆µ„
»∆µ„![]() –˝◊™µΩ»ÁÕº3µƒŒª÷√ ±£¨œþ∂Œ
–˝◊™µΩ»ÁÕº3µƒŒª÷√ ±£¨œþ∂Œ![]() ∫Õ
∫Õ![]() ÷ƺ‰”÷”–‘ı—˘µƒ ˝¡øπÿœµ£ø«Î÷±Ω”–¥≥ˆƒ„µƒ≤¬œÎ£Æ
÷ƺ‰”÷”–‘ı—˘µƒ ˝¡øπÿœµ£ø«Î÷±Ω”–¥≥ˆƒ„µƒ≤¬œÎ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™πÿ”⁄xµƒ“ª‘™∂˛¥Œ∑Ω≥Ãkx2©Å2£®k+1£©x+k©Å1£Ω0”–¡Ω∏ˆ≤ªœýµ»µƒ µ ˝∏˘x1£¨x2£Æ
£®1£©«Ûkµƒ»°÷µ∑∂Œß£ª
£®2£© «∑ҥʑ⁄ µ ˝k£¨ π![]() £Ω1≥…¡¢£ø»Ù¥Ê‘⁄£¨«Î«Û≥ˆkµƒ÷µ£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
£Ω1≥…¡¢£ø»Ù¥Ê‘⁄£¨«Î«Û≥ˆkµƒ÷µ£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨“ª¥Œ∫Ø ˝![]()
![]() µƒÕºœÛ”Î∑¥±»¿˝∫Ø ˝
µƒÕºœÛ”Î∑¥±»¿˝∫Ø ˝![]()
![]() µƒÕºœÛœýΩª”⁄µ⁄“ª°¢»˝œÛœÞƒ⁄µƒ
µƒÕºœÛœýΩª”⁄µ⁄“ª°¢»˝œÛœÞƒ⁄µƒ![]() £¨
£¨![]() ¡Ωµ„£¨”Î
¡Ωµ„£¨”Î![]() ÷·Ωª”⁄µ„
÷·Ωª”⁄µ„![]() £Æ
£Æ
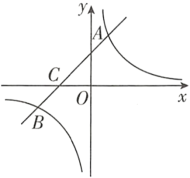
£®1£©«Û∏√∑¥±»¿˝∫Ø ˝∫Õ“ª¥Œ∫Ø ˝µƒΩ‚Œˆ Ω£ª
£®2£©‘⁄![]() ÷·…œ’““ªµ„
÷·…œ’““ªµ„![]() π
π![]() ◊Ó¥Û£¨«Û
◊Ó¥Û£¨«Û![]() µƒ◊Ó¥Û÷µº∞µ„
µƒ◊Ó¥Û÷µº∞µ„![]() µƒ◊¯±Í£Æ
µƒ◊¯±Í£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øπ§≥ߺ◊°¢““¡Ω∏ˆ≤ø√≈∏˜”–‘±π§400»À£¨Œ™¡ÀΩ‚’‚¡Ω∏ˆ≤ø√≈‘±π§µƒ…˙≤˙ººƒÐ«Èøˆ£¨Ω¯––¡À≥È—˘µ˜≤È£¨«ÎΩ´œ¬¡–π˝≥Ã≤π≥‰ÕÍ’˚£∫
’ºØ ˝æð£∫
¥”º◊°¢““¡Ω∏ˆ≤ø√≈∏˜Àʪ˙≥È»°20√˚‘±π§£¨Ω¯––¡À…˙≤˙ººƒÐ≤‚ ‘£¨≤‚ ‘≥…º®£®∞Ÿ∑÷÷∆£©»Áœ¬£∫

’˚¿Ì°¢√Ë ˆ ˝æð£∫
∞¥»Áœ¬∑÷ ˝∂Œ’˚¿Ì°¢√Ë ˆ’‚¡Ω◊È—˘±æ ˝æð£∫
≥…º® »À ˝ ≤ø√≈ | 40°Ðx°Ð49 | 50°Ðx°Ð59 | 60°Ðx°Ð69 | 70°Ðx°Ð79 | 80°Ðx°Ð89 | 90°Ðx°Ð100 |
º◊ | 0 | 0 | 1 | 11 | 7 | 1 |
““ |
£®Àµ√˜£∫≥…º®80∑÷º∞“‘…œŒ™…˙≤˙ººƒÐ”≈–„£¨70°™79∑÷Œ™…˙≤˙ººƒÐ¡º∫√£¨60°™69∑÷Œ™…˙≤˙ººƒÐ∫œ∏Ò£¨60∑÷“‘œ¬Œ™…˙≤˙ººƒÐ≤ª∫œ∏Ò£©
∑÷Œˆ ˝æð£∫
¡Ω◊È—˘±æ ˝æðµƒ∆Ωæ˘ ˝°¢÷–Œª ˝°¢÷⁄ ˝»Áœ¬±ÌÀ˘ æ£∫
≤ø√≈ | ∆Ωæ˘ ˝ | ÷–Œª ˝ | ÷⁄ ˝ |
º◊ | 78£Æ3 | 77£Æ5 | |
““ | 78 | 81 |
µ√≥ˆΩ·¬€£∫
![]() £Æπ¿º∆““≤ø√≈…˙≤˙ººƒÐ”≈–„µƒ‘±π§»À ˝‘ºŒ™ £Æ
£Æπ¿º∆““≤ø√≈…˙≤˙ººƒÐ”≈–„µƒ‘±π§»À ˝‘ºŒ™ £Æ
![]() £Æø…“‘Õ∆∂œ≥ˆ ≤ø√≈‘±π§µƒ…˙≤˙ººƒÐÀÆ∆Ω∏þ£Æ¿Ì”…Œ™ £Æ
£Æø…“‘Õ∆∂œ≥ˆ ≤ø√≈‘±π§µƒ…˙≤˙ººƒÐÀÆ∆Ω∏þ£Æ¿Ì”…Œ™ £Æ
£®÷¡…Ÿ¥”¡Ω∏ˆ≤ªÕ¨µƒΩ«∂»Àµ√˜Õ∆∂œµƒ∫œ¿Ì–‘£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“ª∏ˆ≤ªÕ∏√˜µƒ≤º¥¸÷–Ωˆ”–2∏ˆ∫Ï«Ú°¢1∏ˆ∫⁄«Ú£¨’‚–©«Ú≥˝—’…´Õ‚ŒÞ∆‰À˚≤Ó±£Æ
£®1£©º◊Õ¨—ßœ»Àʪ˙√˛≥ˆ“ª∏ˆ–°«Ú£¨º«œ¬—’…´∫Û∑≈ªÿΩ¡‘»£¨‘ŸÀʪ˙√˛≥ˆ“ª∏ˆ–°«Ú£¨‘Ú¡Ω¥Œ√˛≥ˆµƒ–°«Ú—’…´≤ªÕ¨µƒ∏≈¬ «∂ý…Ÿ£ø
£®2£©““Õ¨—ߥ”÷–“ª¥Œ√˛≥ˆ¡Ω∏ˆ«Ú£¨‘Ú√˛≥ˆµƒ–°«Úæ˘Œ™∫Ï…´µƒ∏≈¬ «___ _.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™¡ÀΩ‚ƒ≥∞ý—ß…˙√øÃÏ π”√¡„ª®«Æµƒ«Èøˆ£¨–°√˜Àʪ˙µ˜≤È¡À15√˚Õ¨—ߣ¨Ω·π˚»Á±Ì£∫
√øÃÏ π”√¡„ª®«Æ£®µ•Œª£∫‘™£© | 0 | 2 | 3 | 4 | 5 |
»À ˝ | 1 | 4 | 5 | 3 | 2 |
πÿ”⁄’‚15√˚Õ¨—ß√øÃÏ π”√¡„ª®«Æµƒ«Èøˆ£¨œ¬¡–Àµ∑®’˝»∑µƒ «£®°°°°£©
A.÷–Œª ˝ «3‘™B.÷⁄ ˝ «5‘™
C.∆Ωæ˘ ˝ «2.5‘™D.∑Ω≤Ó «4
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
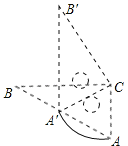
°æƒø°ø»ÁÕº£¨°˜ABC∫Õ°˜A°‰B°‰C «¡Ω∏ˆÕÍ»´÷ÿ∫œµƒ÷±Ω«»˝Ω«∞£¨°œB=30°„£¨–±±þ≥§Œ™10cm£Æ»˝Ω«∞ÂA°‰B°‰C»∆÷±Ω«∂•µ„CÀ≥ ±’Ζ˝◊™£¨µ±µ„A°‰¬‰‘⁄AB±þ…œ ±£¨CA°‰–˝◊™À˘ππ≥…µƒ…»–Œµƒª°≥§Œ™ cm£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com