
【题目】甲、乙两个仓库共存有粮食60![]() .解决下列问题,3个小题都要写出必要的解题过程:
.解决下列问题,3个小题都要写出必要的解题过程:
(1)甲仓库运进粮食14![]() ,乙仓库运出粮食10
,乙仓库运出粮食10![]() 后,两个仓库的粮食数量相等.甲、乙两个仓库原来各有多少粮食?
后,两个仓库的粮食数量相等.甲、乙两个仓库原来各有多少粮食?
(2)如果甲仓库原有的粮食比乙仓库的2倍少3![]() ,则甲仓库运出多少
,则甲仓库运出多少![]() 粮食给乙仓库,可使甲、乙两仓库粮食数量相等?
粮食给乙仓库,可使甲、乙两仓库粮食数量相等?
(3)甲乙两仓库同时运进粮食,甲仓库运进的数量比本仓库原存粮食数量的一半多1![]() ,乙仓库运进的数量是本仓库原有粮食数量加上8
,乙仓库运进的数量是本仓库原有粮食数量加上8![]() 所得的和的一半.求此时甲、乙两仓库共有粮食多少
所得的和的一半.求此时甲、乙两仓库共有粮食多少![]() ?
?
【答案】(1)原来甲仓库有18t粮食,乙仓库有42t粮食;(2)甲仓库运出9t粮食给乙仓库,可使甲、乙两仓库粮食数量相等(3)甲乙两仓库共存有粮食95t
【解析】试题分析:(1)设甲有xt,则乙有(60-x)t,根据甲仓库运进粮食14t,乙仓库运出粮食10t后,两个仓库的粮食数量相等,可得出方程,解出即可;
(2)先求出甲乙粮仓原有多少粮食,再求甲运出的粮食数量即可;
(3)根据题意列出代数式求值 即可.
试题解析:(1)设甲仓库原有粮食xt,则乙仓库原有粮食(60-x)t,
由题知x+14=(60-x)-10,解得x=18.
当x=18时,60-x=42.
∴原来甲仓库有18t粮食,乙仓库有42t粮食;
(2)设甲仓库原有粮食xt,则乙仓库原有粮食(60-x)t,
由题知x=2(60-x)-3,解得x=39.
当x=39时,60-x=21.
∴原来甲仓库有39t粮食,乙仓库有21t粮食.
设甲仓库运出yt粮食给乙仓库,可使甲、乙两仓库粮食数量相等,
由题知39-y=21+y,解得y=9,
∴甲仓库运出9t粮食给乙仓库,可使甲、乙两仓库粮食数量相等.
(3)设甲仓库原有粮食xt,乙仓库原有粮食yt,则x+y=60.
设运进粮食后,两仓库共有粮食wt,则
w=60+(![]() x+1)+
x+1)+![]() (y+8)=65+
(y+8)=65+![]() (x+y)=65+30=95,
(x+y)=65+30=95,
∴此时甲乙两仓库共存有粮食95t.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图1,在边长为4的正△ABC中,点P以每秒1cm的速度从点A出发,沿折线AB﹣BC运动,到点C停止.过点P作PD⊥AC,垂足为D,PD的长度y(cm)与点P的运动时间x(秒)的函数图象如图2所示.当点P运动5.5秒时,PD的长是( )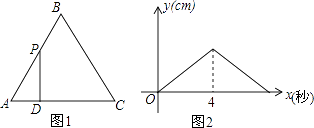
A.![]() cm
cm
B.![]() cm
cm
C.2 ![]() cm
cm
D.3 ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD,AB=9,AD=4. E为CD边上一点,CE=6.
(1)求AE的长.
(2)点P从点B出发,以每秒1个单位的速度沿着边BA向终点A运动,连接PE. 设点P运动的时间为t秒,则当t为何值时,△PAE为等腰三角形?
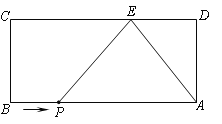
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在“课外新世界”中遇到这样一道题:如图1,已知∠AOB=30°与线段a,你能作出边长为a的等边三角形△COD吗?小明的做法是:如图2,以O为圆心,线段a为半径画弧,分别交OA,OB于点M,N,在弧MN上任取一点P,以点M为圆心,MP为半径画弧,交弧CD于点C,同理以点N为圆心,N P为半径画弧,交弧CD于点D,连结CD,即△COD就是所求的等边三角形. 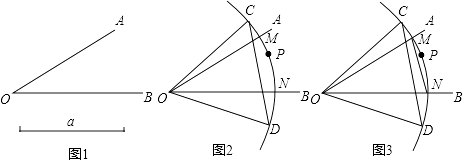
(1)请写出小明这种做法的理由;
(2)在此基础上请你作如下操作和探究(如图3):连结MN,MN是否平行于CD?为什么?
(3)点P在什么位置时,MN∥CD?请用小明的作图方法在图1中作出图形(不写作法,保留作图痕迹).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 两边同除以
两边同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣![]() 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).
错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新华书店举行购书优惠活动
①一次性购书不超过100元,不享受打折优惠
②一次性购书超过100元但不超过200元一律打九折;
③一次性购书200元以上一律打七折
小丽在这次活动中,两次购书总共付款240.87元,第二次购书原价是第一次购书原价的3倍,那么小丽这两次购书原价的总和是_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知实数a,b,c满足(a-![]() )2+
)2+![]() +|c-2
+|c-2![]() |=0.
|=0.
(1)求a,b,c的值;
(2)试问以a,b,c为边能否构成三角形?若能构成三角形,求出三角形的周长和面积;若不能构成三角形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意四个有理数a,b,c,d,可以组成两个有理数对(a,b)与(c,d).我们规定:
(a,b)★(c,d)=bc﹣ad.
例如:(1,2)★(3,4)=2×3﹣1×4=2.
根据上述规定解决下列问题:
(1)有理数对(2,﹣3)★(3,﹣2)= ;
(2)若有理数对(﹣3,2x﹣1)★(1,x+1)=7,则x= ;
(3)当满足等式(﹣3,2x﹣1)★(k,x+k)=5+2k的x是整数时,求整数k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com