
【题目】已知抛物线y=ax2+bx﹣3经过(﹣1,0),(3,0)两点,与y轴交于点C,直线y=kx与抛物线交于A,B两点.
(1)写出点C的坐标并求出此抛物线的解析式;
(2)当原点O为线段AB的中点时,求k的值及A,B两点的坐标;
(3)是否存在实数k使得△ABC的面积为![]() ?若存在,求出k的值;若不存在,请说明理由.
?若存在,求出k的值;若不存在,请说明理由.

【答案】(1)y=x2﹣2x﹣3;(2)当原点O为线段AB的中点时,k的值为﹣2,点A的坐标为(﹣![]() ,2
,2![]() ),点B的坐标为(
),点B的坐标为(![]() ,﹣2
,﹣2![]() ).(3)不存在,理由详见解析.
).(3)不存在,理由详见解析.
【解析】
试题分析:(1)令x=0求出y值即可得出C点的坐标,又有点(﹣1,0)、(3,0),利用待定系数法求抛物线的解析式即可;(2)将正比例函数解析式代入抛物线解析式中,找出关于x的一元二次方程,根据根与系数的关系即可得出“xA+xB=2+k,xAxB=﹣3”,结合点O为线段AB的中点即可得出xA+xB=2+k=0,由此得出k的值,将k的值代入一元二次方程中求出xA、xB,在代入一次函数解析式中即可得出点A、B的坐标;(3)假设存在,利用三角形的面积公式以及(2)中得到的“xA+xB=2+k,xAxB=﹣3”,即可得出关于k的一元二次方程,结合方程无解即可得出假设不成立,从而得出不存在满足题意的k值.
试题解析:(1)令抛物线y=ax2+bx﹣3中x=0,则y=﹣3,
∴点C的坐标为(0,﹣3).
∵抛物线y=ax2+bx﹣3经过(﹣1,0),(3,0)两点,
∴有![]() ,解得:
,解得:![]() ,
,
∴此抛物线的解析式为y=x2﹣2x﹣3.
(2)将y=kx代入y=x2﹣2x﹣3中得:kx=x2﹣2x﹣3,
整理得:x2﹣(2+k)x﹣3=0,
∴xA+xB=2+k,xAxB=﹣3.
∵原点O为线段AB的中点,
∴xA+xB=2+k=0,
解得:k=﹣2.
当k=﹣2时,x2﹣(2+k)x﹣3=x2﹣3=0,
解得:xA=﹣![]() ,xB=
,xB=![]() .
.
∴yA=﹣2xA=2![]() ,yB=﹣2xB=2
,yB=﹣2xB=2![]() .
.
故当原点O为线段AB的中点时,k的值为﹣2,点A的坐标为(﹣![]() ,2
,2![]() ),点B的坐标为(
),点B的坐标为(![]() ,﹣2
,﹣2![]() ).
).
(3)假设存在.
由(2)可知:xA+xB=2+k,xAxB=﹣3,
S△ABC=![]() OC|xA﹣xB|=
OC|xA﹣xB|=![]() ×3×
×3×![]() =
=![]() ,
,
∴(2+k)2﹣4×(﹣3)=10,即(2+k)2+2=0.
∵(2+k)2非负,无解.
故假设不成立.
所以不存在实数k使得△ABC的面积为![]() .
.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】桌上倒扣着背面相同的5张扑克牌,其中3张黑桃、2张红桃.从中随机抽取一张,则( )
A.能够事先确定抽取的扑克牌的花色
B.抽到黑桃的可能性更大
C.抽到黑桃和抽到红桃的可能性一样大
D.抽到红桃的可能性更大
查看答案和解析>>
科目:初中数学 来源: 题型:
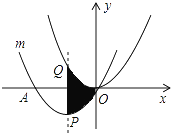
【题目】如图,把抛物线y=![]() x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=
x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=![]() x2交于点Q,则图中阴影部分的面积为________.
x2交于点Q,则图中阴影部分的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解本校九年级男生“引体向上”项目的训练情况,随机抽取该年级部分男生进行了一次测试(满分15分,成绩均记为整数分),并按测试成绩(单位:分)分成四类:A类(12≤m≤15),B类(9≤m≤11),C类(6≤m≤8),D类(m≤5)绘制出以下两幅不完整的统汁图,请根据图中信息解答下列问题:
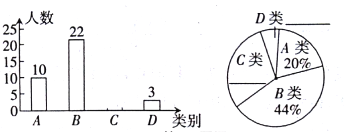
(l)本次抽取样本容量为____,扇形统计图中A类所对的圆心角是____度;
(2)请补全统计图;
(3)若该校九年级男生有300名,请估计该校九年级男生“引体向上”项目成绩为C类的有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A.在一个三角形中,至多有两个内角是钝角
B.三角形的两边之和小于第三边
C.在一个三角形中,至多有两个内角是锐角
D.在同一平面内,垂直于同一直线的两直线平行
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com