
【题目】如图,已知正方形ABCD中,∠MAN=45°,连接BD与AM,AN分别交于E,F点,则下列结论正确的有_____.
①MN=BM+DN
②△CMN的周长等于正方形ABCD的边长的两倍;
③EF2=BE2+DF2;
④点A到MN的距离等于正方形的边长
⑤△AEN、△AFM都为等腰直角三角形.
⑥S△AMN=2S△AEF
⑦S正方形ABCD:S△AMN=2AB:MN
⑧设AB=a,MN=b,则![]() ≥2
≥2![]() ﹣2.
﹣2.

【答案】①②③④⑤⑥⑦.
【解析】
将△ABM绕点A逆时针旋转,使AB与AD重合,得到△ADH.证明△MAN≌△HAN,得到MN=NH,根据三角形周长公式计算判断①;判断出BM=DN时,MN最小,即可判断出⑧;根据全等三角形的性质判断②④;将△ADF绕点A顺时针性质90°得到△ABH,连接HE.证明△EAH≌△EAF,得到∠HBE=90°,根据勾股定理计算判断③;根据等腰直角三角形的判定定理判断⑤;根据等腰直角三角形的性质、三角形的面积公式计算,判断⑥,根据点A到MN的距离等于正方形ABCD的边长、三角形的面积公式计算,判断⑦.
将△ABM绕点A逆时针旋转,使AB与AD重合,得到△ADH.
则∠DAH=∠BAM,
∵四边形ABCD是正方形,
∴∠BAD=90°,
∵∠MAN=45°,
∴∠BAN+∠DAN=45°,
∴∠NAH=45°,
在△MAN和△HAN中,
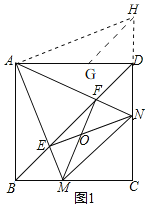
 ,
,
∴△MAN≌△HAN,
∴MN=NH=BM+DN,①正确;
∵BM+DN≥2![]() ,(当且仅当BM=DN时,取等号)
,(当且仅当BM=DN时,取等号)
∴BM=DN时,MN最小,
∴BM=![]() b,
b,
∵DH=BM=![]() b,
b,
∴DH=DN,
∵AD⊥HN,
∴∠DAH=![]() ∠HAN=22.5°,
∠HAN=22.5°,
在DA上取一点G,使DG=DH=![]() b,
b,
∴∠DGH=45°,HG=![]() DH=
DH=![]() b,
b,
∵∠DGH=45°,∠DAH=22.5°,
∴∠AHG=∠HAD,
∴AG=HG=![]() b,
b,
∴AB=AD=AG+DG=![]() b+
b+![]() b=
b=![]() b=a,
b=a,
∴![]() ,
,
∴![]() ,
,
当点M和点B重合时,点N和点C重合,此时,MN最大=AB,
即:![]() ,
,
∴![]() ≤
≤![]() ≤1,⑧错误;
≤1,⑧错误;
∵MN=NH=BM+DN
∴△CMN的周长=CM+CN+MN=CM+BM+CN+DN=CB+CD,
∴△CMN的周长等于正方形ABCD的边长的两倍,②结论正确;
∵△MAN≌△HAN,
∴点A到MN的距离等于正方形ABCD的边长AD,④结论正确;
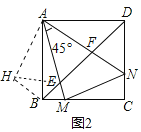
如图2,将△ADF绕点A顺时针性质90°得到△ABH,连接HE.
∵∠DAF+∠BAE=90°-∠EAF=45°,∠DAF=∠BAE,
∴∠EAH=∠EAF=45°,
∵EA=EA,AH=AD,
∴△EAH≌△EAF,
∴EF=HE,
∵∠ABH=∠ADF=45°=∠ABD,
∴∠HBE=90°,
在Rt△BHE中,HE2=BH2+BE2,
∵BH=DF,EF=HE,
∵EF2=BE2+DF2,③结论正确;
∵四边形ABCD是正方形,
∴∠ADC=90°,∠BDC=∠ADB=45°,
∵∠MAN=45°,
∴∠EAN=∠EDN,
∴A、E、N、D四点共圆,
∴∠ADN+∠AEN=180°,
∴∠AEN=90°
∴△AEN是等腰直角三角形,
同理△AFM是等腰直角三角形;⑤结论正确;
∵△AEN是等腰直角三角形,同理△AFM是等腰直角三角形,
∴AM=![]() AF,AN=
AF,AN=![]() AE,
AE,
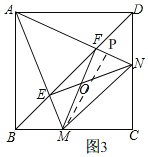
如图3,过点M作MP⊥AN于P,
在Rt△APM中,∠MAN=45°,
∴MP=AMsin45°,
∵S△AMN=![]() ANMP=
ANMP=![]() AMANsin45°,
AMANsin45°,
S△AEF=![]() AEAFsin45°,
AEAFsin45°,
∴S△AMN:S△AEF=2,
∴S△AMN=2S△AEF,⑥正确;
∵点A到MN的距离等于正方形ABCD的边长,
∴S正方形ABCD:S△AMN=![]() =2AB:MN,⑦结论正确.
=2AB:MN,⑦结论正确.
即:正确的有①②③④⑤⑥⑦,
故答案为①②③④⑤⑥⑦.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】已知方程![]() +px+q=0的两个根是
+px+q=0的两个根是![]() ,
,![]() ,那么
,那么![]() +
+![]() =-p,
=-p,![]()
![]() =q,反过来,如果
=q,反过来,如果![]() +
+![]() =-p,
=-p,![]()
![]() =q,那么以
=q,那么以![]() ,
,![]() 为两根的一元二次方程是
为两根的一元二次方程是![]() +px+q=0.请根据以上结论,解决下列问题:
+px+q=0.请根据以上结论,解决下列问题:
(1)已知关于x的方程![]() +mx+n=0(n≠0),求出—个一元二次方程,使它的两根分别是已知方程两根的倒数.
+mx+n=0(n≠0),求出—个一元二次方程,使它的两根分别是已知方程两根的倒数.
(2)已知a、b满足![]() -15a-5=0,
-15a-5=0,![]() -15b-5=0,求
-15b-5=0,求![]() 的值.
的值.
(3)已知a、b、c均为实数,且a+b+c=0,abc=16,求正数c的最小值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线AB分别与x轴、y轴交于A、B两点,OC平分∠AOB交AB于点C,点D为线段AB上一点,过点D作DE∥OC交y轴于点E,已知AO=m,BO=n,且m、n满足n2﹣12n+36+|n﹣2m|=0.

(1)求A、B两点的坐标;
(2)若点D为AB中点,延长DE交x轴于点F,在ED的延长线上取点G,使DG=DF,连接BG.
①BG与y轴的位置关系怎样?说明理由; ②求OF的长;
(3)如图2,若点F的坐标为(10,10),E是y轴的正半轴上一动点,P是直线AB上一点,且P的横坐标为6,是否存在点E使△EFP为等腰直角三角形?若存在,求出点E的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 和
和![]() ,
,![]() .
.
![]() 画出矩形
画出矩形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后的矩形
后的矩形![]() ,并写出
,并写出![]() 的坐标为________,点
的坐标为________,点![]() 运动到点
运动到点![]() 所经过的路径的长为________;
所经过的路径的长为________;
![]() 若点
若点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为________,请画一条直线
的坐标为________,请画一条直线![]() 平分矩形
平分矩形![]() 与
与![]() 组成图形的面积(保留必要的画图痕迹).
组成图形的面积(保留必要的画图痕迹).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面内,若点P与△ABC三个顶点中的任意两个顶点连接形成的三角形都是等腰三角形,则称点P是△ABC的巧妙点.
(1)如图1,求作△ABC的巧妙点P(尺规作图,不写作法,保留作图痕迹).

(2)如图2,在△ABC中,∠A=80°,AB=AC,求作△ABC的所有巧妙点P (尺规作图,不写作法,保留作图痕迹),并直接写出∠BPC的度数是 .

(3)等边三角形的巧妙点的个数有( )
A.2 B.6 C.10 D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=(x-1)2-1.
(1)该抛物线的对称轴是______________,顶点坐标为____________;
(2)选取适当的数据填入下表,并在图中的直角坐标系内描点画出该抛物线;
x | … | … | |||||
y | … | … |

(3)根据图象,直接写出当y<0时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ΔABC中,AD是高,AE、BF是角平分线,它们相交与点O,∠BAC=50°,∠C=70°,则∠DAC的度数为__________,∠BOA的度数为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边上的中点,将
边上的中点,将![]() 绕点
绕点![]() 顺时针旋转,旋转角为
顺时针旋转,旋转角为![]() 得到
得到![]() ,
,![]() 的两边分别与
的两边分别与![]() 、
、![]() 边相交于点
边相交于点![]() ,
,![]() 两点,连结
两点,连结![]() .
.
(1)求证:![]() ;
;
(2)求![]() 的度数;
的度数;
(3)当![]() 变成等腰直角三角形时,求
变成等腰直角三角形时,求![]() 的长;
的长;
(4)在此运动变化的过程中,四边形![]() 的面积是否保持不变?试说明理由.
的面积是否保持不变?试说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com