
【题目】如图,边长为4的正方形ABCD外切于⊙O,切点分别为E、F、G、H.则图中阴影部分的面积为______.

 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】某商店销售一种销售成本为每千克30元的水产品,据市场分析,若按每千克40元销售,一个月能售出500千克;销售单价每涨1元,月销售量就减少10千克,针对这种情况,请解答以下问题:
(1)当销售单价定为每千克45元时,计算月销售量和月销售利润;
(2)该商店想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应定为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解居民月用水量,某市对某区居民用水量进行了抽样调查,并制成如下直方图.

(1)这次一共抽查了____户;
(2)用水量不足10吨的有____户,用水量超过16吨的有____户;
(3)假设该区有8万户居民,估计用水量少于10吨的有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,AE=CD,AD,BE相交于点P,BQ⊥AD于点Q.
(1)求证:BP=2PQ;
(2)若PE=1,PQ=3,试求AD的长.
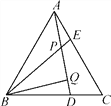
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产A,B两种产品共10件,其中A种产品的生产成本为每件3万元,B种产品的生产成本为每件5万元;并且销售一件A种产品的利润为1万元,销售一件B种产品的利润为2万元。
(1)若工厂计划获得总利润为14万元,问A,B两种产品应分别生产多少件?
(2)若工厂投入两种产品的总生产成本不多于44万元,且获得总利润多于14万元,问工厂有哪几种生产方案(即A,B两种产品各生产多少件)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=
ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=![]() ,则梯形AECD的周长为( )
,则梯形AECD的周长为( )
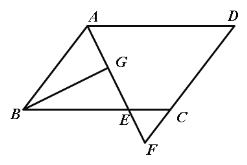
A.22 B.23 C.24 D.25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)先完成下列表格:
a | …… | 0.0001 | 0.01 | 1 | 100 | 10000 | …… |
| …… | 0.01 | ______ | 1 | ______ | ______ | …… |
(2)由上表你发现什么规律?
(3)根据你发现的规律填空:
①已知![]() =1.732则
=1.732则![]() =______
=______![]() =______
=______
②已知![]() =0.056,则
=0.056,则![]() =______
=______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为做好“家电下乡”的惠民服务,决定从厂家购进甲、乙、丙三种不同型号的电视机108台,其中甲种电视机的台数是丙种的4倍,购进三种电视机的总金额不超过147 000元,已知甲、乙、丙三种型号的电视机的出厂价格分别为1 000元/台,1 500元/台,2 000元/台.
(1)求该商场至少购买丙种电视机多少台?
(2)若要求甲种电视机的台数不超过乙种电视机的台数,问有哪些购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() ;那么
;那么![]() 与
与![]() 平行吗?试说明理由.
平行吗?试说明理由.

请将下面的推理过程补充完整.
解:![]() ,理由如下:
,理由如下:
![]() (已知)
(已知)
![]() (平角的定义)
(平角的定义)
![]() ( )
( )
![]()
![]() ( )
( )
![]() (两直线平行,同位角相等)
(两直线平行,同位角相等)
![]() (已知)
(已知)
![]() ( )
( )
![]() (内错角相等,两直线平行)
(内错角相等,两直线平行)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com