
 如图,等边△ABC,D、E分别在AB、AC边上,且AD=CE,G为DE中点,FG⊥DE交BC于F,求证:CF=AE.
如图,等边△ABC,D、E分别在AB、AC边上,且AD=CE,G为DE中点,FG⊥DE交BC于F,求证:CF=AE. 分析 在BC上截取CM=AE,即可证明△ADE≌△CED,然后证明△BDM≌△△CME,则DM=DE,即M在DE的垂直平分线上,然后根据FG是DE的垂直平分线,即可证明M和F重合,即可证得.
解答 证明: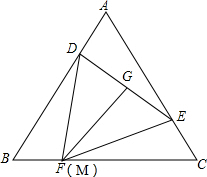 在BC上截取CM=AE.
在BC上截取CM=AE.
∵△ABC是等边三角形,
∴∠A=∠C=60°,
在△ADE和△CEM中,
$\left\{\begin{array}{l}{AD=CE}\\{∠A=∠C}\\{AE=CM}\end{array}\right.$,
∴△ADE≌△CEM,
∴AD=BM.
又∵等边△ABC中,AB=BC,
∴BD=CM,
同理可证△BDM≌△△CME,
∴DM=ME,
∴M在DE的垂直平分线上.
又∵G为DE中点,FG⊥DE交BC于F,即FG是线段DE的垂直平分线,
∴F和M重合,
∴CF=AE.
点评 本题考查了全等三角形的判定与性质,以及线段的垂直平分线的性质,理解同一法证明的思路是本题的关键.


科目:初中数学 来源: 题型:解答题
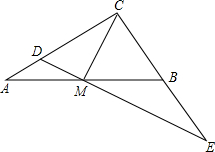 已知:如图,在△ABC中,∠ACB=90°,CM是斜边AB上的中线.
已知:如图,在△ABC中,∠ACB=90°,CM是斜边AB上的中线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 由于现在人们生活水平的普遍提高,大家对自己的生存环境越来越关注,特别是对大气环境质量的关注,而空气中又以PM2.5对人体的危害性最大,某市环保局对该市市民进行了一项民意调查,以了解PM2.5浓度升高时对人们户外活动是否有影响,并制作了统计图表的一部分如下:
由于现在人们生活水平的普遍提高,大家对自己的生存环境越来越关注,特别是对大气环境质量的关注,而空气中又以PM2.5对人体的危害性最大,某市环保局对该市市民进行了一项民意调查,以了解PM2.5浓度升高时对人们户外活动是否有影响,并制作了统计图表的一部分如下:| 公众对于户外活动的态度 | 百分比 |
| A.没有影响 | a |
| B.影响不大,还可以进行户外活动 | 5% |
| C.有影响,减少户外活动 | 42% |
| D.影响很大,尽可能不去户外活动 | b |
| E.不关心这个问题 | 6% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,C,F是线段BE上的两点,△ABF≌△DEC,且AC=DF.
如图,C,F是线段BE上的两点,△ABF≌△DEC,且AC=DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,等腰Rt△ABC中,AB=AC,∠BAC=90°,BE平分∠ABC交AC于E,过C作CD⊥BE于D,DM⊥AB交BA的延长线于M,连接DA,
如图,等腰Rt△ABC中,AB=AC,∠BAC=90°,BE平分∠ABC交AC于E,过C作CD⊥BE于D,DM⊥AB交BA的延长线于M,连接DA,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com