
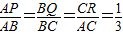 ,求
,求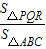 的值.
的值.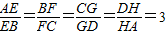 ,求
,求 的值.
的值.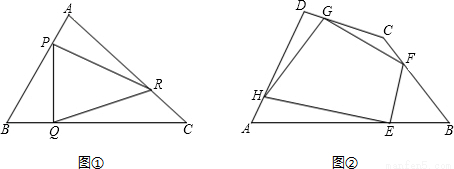
 AB,BQ=
AB,BQ= BC,CR=
BC,CR= AC,BP=
AC,BP= AB,CQ=
AB,CQ= BC,AR=
BC,AR= AC;然后利用三角形的面积公式S=
AC;然后利用三角形的面积公式S= absinC求得△ABC中除去△PQR的三个小三角形的面积与△ABC的面积间的数量关系;最后由S△PQR=S△ABC-S△APR-S△BPQ-S△CQR=
absinC求得△ABC中除去△PQR的三个小三角形的面积与△ABC的面积间的数量关系;最后由S△PQR=S△ABC-S△APR-S△BPQ-S△CQR= S△ABC可以推知
S△ABC可以推知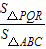 的值;
的值;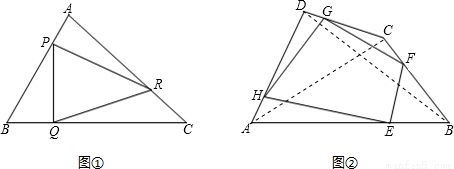 解:(1)∵P,Q,R是△ABC三边上的点,且
解:(1)∵P,Q,R是△ABC三边上的点,且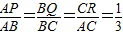 ,
, AB,BQ=
AB,BQ= BC,CR=
BC,CR= AC,
AC, AB,CQ=
AB,CQ= BC,AR=
BC,AR= AC,
AC, AP•ARsinA=
AP•ARsinA= ×
× AB•
AB• AC•sinA=
AC•sinA= ×
× AB•ACsinA=
AB•ACsinA= S△ABC;
S△ABC; BQ•BPsinB=
BQ•BPsinB= ×
× BC•
BC• AB•sinB=
AB•sinB= ×
× BC•ABsinB=
BC•ABsinB= S△ABC;
S△ABC; CR•CQsinC=
CR•CQsinC= ×
× AC•
AC• BC•sinC=
BC•sinC= ×
× AC•BCsinC=
AC•BCsinC= S△ABC;
S△ABC; S△ABC,
S△ABC,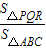 =
= ;
;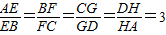 ,
, AB,AH=
AB,AH= AD,CF=
AD,CF= BC,CG=
BC,CG= CD,
CD, AE•AHsin∠HAE=
AE•AHsin∠HAE= ×
× AB×
AB× ADsin∠HAE=
ADsin∠HAE=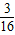 ×
× AB•ADsin∠HAE=
AB•ADsin∠HAE=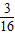 S△ABD,
S△ABD, CF•CGsin∠DCB=
CF•CGsin∠DCB= ×
× CD×
CD× BCsin∠DCB=
BCsin∠DCB=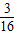 ×
× CD•BCsin∠DCB=
CD•BCsin∠DCB=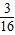 S△CDB,
S△CDB,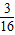 (S△ABD+S△CDB)=
(S△ABD+S△CDB)=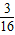 S四边形ABCD;
S四边形ABCD;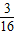 (S△ADC+S△ABC)=
(S△ADC+S△ABC)=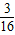 S四边形ABCD;
S四边形ABCD; S四边形EFGH,
S四边形EFGH, =
= .
.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 如图,已知A,B两点是反比例函数y=
如图,已知A,B两点是反比例函数y=| 4 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com