
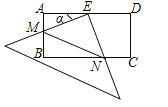
【题目】在矩形ABCD中,AD=2AB=4,E是AD的中点,一块足够大的三角板的直角顶点与点E重合,将三角板绕点E旋转,三角板的两直角边分别交AB,BC(或它们的延长线)于点M,N,设∠AEM=α(0°<α<90°),给出下列四个结论:
①AM=CN;②∠AME=∠BNE;③BN﹣AM=2;④S△EMN=![]() .
.
上述结论中正确的个数是( )
A.1 B.2 C.3 D.4
【答案】C.
【解析】
试题分析:①如图,在矩形ABCD中,AD=2AB,E是AD的中点,作EF⊥BC于点F,则有AB=AE=EF=FC,∵∠AEM+∠DEN=90°,∠FEN+∠DEN=90°,∴∠AEM=∠FEN,在Rt△AME和Rt△FNE中,∵∠AEM=∠FEN,AE=EF,∠MAE=∠NFE,∴Rt△AME≌Rt△FNE,∴AM=FN,∴MB=CN.

∵AM不一定等于CN,∴AM不一定等于CN,∴①错误,②由①有Rt△AME≌Rt△FNE,∴∠AME=∠BNE,∴②正确,③由①得,BM=CN,∵AD=2AB=4,∴BC=4,AB=2
∴BN﹣AM=BC﹣CN﹣AM=BC﹣BM﹣AM=BC﹣(BM+AM)=BC﹣AB=4﹣2=2,∴③正确,④如图,
由①得,CN=CF﹣FN=2﹣AM,AE=![]() AD=2,AM=FN
AD=2,AM=FN
∵tanα=![]() ,∴AM=AEtanα
,∴AM=AEtanα
∵cosα=![]() =
=![]() ,∴
,∴ ![]() ,∴
,∴![]() =1+
=1+![]() =1+
=1+![]() =1+
=1+![]() ,∴
,∴![]() =2(1+
=2(1+![]() )
)
∴S△EMN=S四边形ABNE﹣S△AME﹣S△MBN
=![]() (AE+BN)×AB﹣
(AE+BN)×AB﹣![]() AE×AM﹣
AE×AM﹣![]() BN×BM
BN×BM
=![]() (AE+BC﹣CN)×2﹣
(AE+BC﹣CN)×2﹣![]() AE×AM﹣
AE×AM﹣![]() (BC﹣CN)×CN
(BC﹣CN)×CN
=![]() (AE+BC﹣CF+FN)×2﹣
(AE+BC﹣CF+FN)×2﹣![]() AE×AM﹣
AE×AM﹣![]() (BC﹣2+AM)(2﹣AM)
(BC﹣2+AM)(2﹣AM)
=AE+BC﹣CF+AM﹣![]() AE×AM﹣
AE×AM﹣![]() (2+AM)(2﹣AM)
(2+AM)(2﹣AM)
=AE+AM﹣![]() AE×AM+
AE×AM+![]()
![]()
=AE+AEtanα﹣![]()
![]() tanα+
tanα+![]()
![]()
![]()
=2+2tanα﹣2tanα+2![]()
=2(1+![]() )
)
=![]() ,∴④正确.
,∴④正确.
故选C.


科目:初中数学 来源: 题型:
【题目】某校对七、八、九年级的学生进行体育水平测试,成绩评定为优秀、良好、合格、不合格四个等第.为了解这次测试情况,学校从三个年级随机抽取200名学生的体育成绩进行统计分析.相关数据的统计图、表如下:
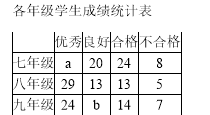
根据以上信息解决下列问题:
(1)在统计表中,a的值为 ,b的值为 ;
(2)在扇形统计图中,八年级所对应的扇形圆心角为 度;
(3)若该校三个年级共有2000名学生参加考试,试估计该校学生体育成绩不合格的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】开学初,小明到某商场购物,发现商场正在进行购物返券活动,活动规则如下:购物每满100元,返购物券50元,此购物券在本商场通用,且用购物券购买商品不再返券.小明只购买了单价分别为60元、80元和120元的书包、T恤、运动鞋,在使用购物券参与购买的情况下,他的实际花费为 元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,DE是边AB的垂直平分线,交AB于E、交AC于D,连接BD.
(1)若∠ABC=∠C,∠A=40°,求∠DBC的度数;
(2)若AB=AC,且△BCD的周长为18cm,△ABC的周长为30cm,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】证明定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等,已知:
如图,在△ABC中,分别作AB边、BC边的垂直平分线,两线相交于点P,分别交AB边、BC边于点E、F.
求证:AB、BC、AC的垂直平分线相交于点P
证明:∵点P是AB边垂直平线上的一点,
∴ = ( ).
同理可得,PB= .
∴ = (等量代换).
∴ (到一条线段两个端点距离相等的点,在这条线段的 )
∴AB、BC、AC的垂直平分线 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向![]() 海里的C处,为了防止某国还巡警干扰,就请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
海里的C处,为了防止某国还巡警干扰,就请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各对数中,结果相等的是( )
A. (﹣3)2与﹣32 B. (﹣3)7与﹣37
C. ﹣(﹣3)2与﹣(﹣2)3 D. |﹣23|与﹣|23|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG。
求证:(1)AD=AG,(2)AD与AG的位置关系如何。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com