
如图,在正方形ABCD中,E是边CD上一点,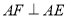 交CB的延长线于点F,联结DF,分别交AE、AB于点G、P.
交CB的延长线于点F,联结DF,分别交AE、AB于点G、P.
(1)求证:AE=AF;
(2)若∠BAF=∠BFD,求证:四边形APED是矩形.
(1)见解析;(2)见解析
【解析】
试题分析:
(1)若要证明AE=AF,则可证明以上两条线段所在的三角形全等即可;
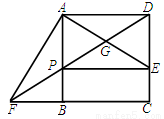
(2)利用正方形的性质以及垂直定义得出∠1=∠3=∠4=∠5,进而利用全等三角形的判定与性质得出AP=DE,进而利用平行四边形的判定以及矩形的判定得出即可.
试题解析:
证明:(1)∵四边形ABCD是正方形,
∴∠ADE=∠ABC=∠DAB=90°,AD=AB,AD∥BC,AB∥CD,
∵AF⊥AE,
∴∠EAF=90°,
∴∠DAE=∠BAF,
在△ADE和△ABF中,
∠DAE=∠BAF ,AD=AB ,∠ADE=∠ABF=90°,
∴△ADE≌△ABF(ASA),
∴AF=AE;
(2)∵AF⊥AE,
∴∠1+∠2=90°,
∵∠2+∠3=90°,
∴∠1=∠3,
∵AD∥FC,
∴∠4=∠5,
∵∠1=∠5,
∴∠1=∠3=∠4=∠5,
在△ADE和△DAP中,
∠3=∠4 ,AD=AD ,∠ADE=∠DAP ,
∴△ADE≌△DAP(ASA),
∴AP=DE,
又∵AP∥DE,
∴四边形APED是平行四边形,
∵∠PAD=90°,
∴平行四边形APED是矩形.
考点:正方形的性质;全等三角形的判定与性质;矩形的判定.


科目:初中数学 来源:2013-2014学年中考数学章节复习测试全等三角形练习卷(解析版) 题型:解答题
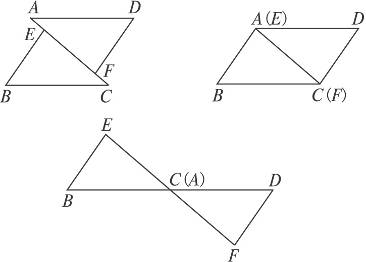
如图,已知AE=CF,∠DAF=∠BCE,AD=CB.
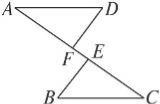
(1)问:△ADF与△CBE全等吗?请说明理由.
(2)如果将△BEC沿CA边方向平行移动,可有图中3幅图,如上面的条件不变,结论仍成立吗?请选择一幅图说明理由.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年上海市浦东新区中考二模数学试卷(解析版) 题型:选择题
已知抛物线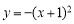 上的两点
上的两点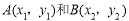 ,如果
,如果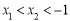 ,那么下列结论一定成立的是
,那么下列结论一定成立的是
(A)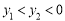 (B)
(B)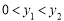 (C)
(C)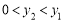 (D)
(D)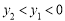 .
.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年上海市毕业生学业模拟考试数学试卷(解析版) 题型:填空题
如图,在Rt△ABC中,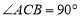 ,AC=4,BC=3,点D为AB的中点,将△ACD绕着点C逆时针旋转,使点A落在CB的延长线
,AC=4,BC=3,点D为AB的中点,将△ACD绕着点C逆时针旋转,使点A落在CB的延长线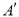 处,点D落在点
处,点D落在点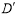 处,则
处,则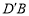 长为 .
长为 .

查看答案和解析>>
科目:初中数学 来源:2013-2014学年上海市杨浦区5月中考二模数学试卷(解析版) 题型:选择题
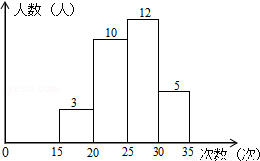
某学校为了了解九年级体能情况,随机选取30名学生测试一分钟仰卧起坐次数,并绘制了如图的直方图,学生仰卧起坐次数在25~30之间的频率为( )
A.0.1 B.0.17 C.0.33 D.0.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com