
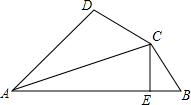
 如图,AC平分∠DAB,CE⊥AB于E,AB=AD+2BE,下列结论正确的有( )个
如图,AC平分∠DAB,CE⊥AB于E,AB=AD+2BE,下列结论正确的有( )个| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 ①在AE取点F,使EF=BE.利用已知条件AB=AD+2BE,可得AD=AF,进而证出2AE=AB+AD;
②在AB上取点F,使BE=EF,连接CF.先由SAS证明△ACD≌△ACF,得出∠ADC=∠AFC;再根据线段垂直平分线、等腰三角形的性质得出∠CFB=∠B;然后由邻补角定义及四边形的内角和定理得出∠DAB+∠DCB=180°;
③根据全等三角形的对应边相等得出CD=CF,根据线段垂直平分线的性质性质得出CF=CB,从而CD=CB;
④由于△CEF≌△CEB,△ACD≌△ACF,根据全等三角形的面积相等易证S△ACE-2S△BCE=S△ADC.
⑤结合①的解题过程进行判断即可.
解答 解:①在AE取点F,使EF=BE,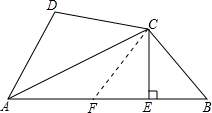
∵AB=AD+2BE=AF+EF+BE,EF=BE,
∴AB=AD+2BE=AF+2BE,
∴AD=AF,
∴AB+AD=AF+EF+BE+AD=2AF+2EF=2(AF+EF)=2AE,
∴AE=$\frac{1}{2}$(AB+AD),故①正确;
②在AB上取点F,使BE=EF,连接CF.
在△ACD与△ACF中,∵AD=AF,∠DAC=∠FAC,AC=AC,
∴△ACD≌△ACF,
∴∠ADC=∠AFC.
∵CE垂直平分BF,
∴CF=CB,
∴∠CFB=∠B.
又∵∠AFC+∠CFB=180°,
∴∠ADC+∠B=180°,
∴∠DAB+∠DCB=360-(∠ADC+∠B)=180°,故②正确;
③由②知,△ACD≌△ACF,∴CD=CF,
又∵CF=CB,
∴CD=CB,故③正确;
④易证△CEF≌△CEB,
∴S△ACE-S△BCE=S△ACE-S△FCE=S△ACF,
又∵△ACD≌△ACF,
∴S△ACF=S△ADC,
∴S△ACE-2S△BCE=S△ADC,故④正确.
⑤由①知,AD=AF,且AF<AE,所以AD<AE,故⑤错误.
故选D.
点评 本题考查了三角形综合题,需要掌握角平分线性质,全等三角形的性质和判定,等腰三角形的性质,四边形的内角和定理,邻补角定义等知识点的应用,正确作辅助线是解此题的关键,综合性比较强,难度适中.


科目:初中数学 来源: 题型:选择题
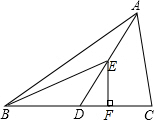 如图,△ABC的面积为40,AD为△ABC的中线,BD=5,BE为△ABD的中线,
如图,△ABC的面积为40,AD为△ABC的中线,BD=5,BE为△ABD的中线,| A. | 2 | B. | 3 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
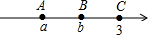 如图,A、B、C在数轴上对应的数分别为a,b和3,AB=BC.若|a|>3,|b|<3,那么原点位置应该在( )
如图,A、B、C在数轴上对应的数分别为a,b和3,AB=BC.若|a|>3,|b|<3,那么原点位置应该在( )| A. | 点A的左边 | B. | 点B和点C之间且靠近点B | ||
| C. | 点C的右边 | D. | 点B和点C之间且靠近点C |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com