
°æƒø°ø»ÁÕº£¨≈◊ŒÔœþy£Ωax2+bx£®a£æ0£©π˝µ„E£®8£¨0£©£¨æÿ–ŒABCDµƒ±þAB‘⁄œþ∂ŒOE…œ£®µ„A‘⁄µ„Bµƒ◊Û≤ý£©£¨µ„C°¢D‘⁄≈◊ŒÔœþ…œ£¨°œBADµƒ∆Ω∑÷œþAMΩªBC”⁄µ„M£¨µ„N «CDµƒ÷–µ„£¨“—÷™OA£Ω2£¨«“OA£∫AD£Ω1£∫3.
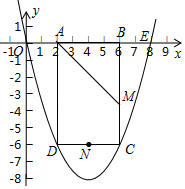
£®1£©«Û≈◊ŒÔœþµƒΩ‚Œˆ Ω£ª
£®2£©F°¢G∑÷±Œ™x÷·£¨y÷·…œµƒ∂ص„£¨À≥¥Œ¡¨Ω”M°¢N°¢G°¢Fππ≥…Àƒ±þ–ŒMNGF£¨«ÛÀƒ±þ–ŒMNGF÷Ð≥§µƒ◊Ó–°÷µ£ª
£®3£©‘⁄x÷·œ¬∑Ω«“‘⁄≈◊ŒÔœþ…œ «∑ҥʑ⁄µ„P£¨ π°˜ODP÷–OD±þ…œµƒ∏þŒ™![]() £ø»Ù¥Ê‘⁄£¨«Û≥ˆµ„Pµƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£ª
£ø»Ù¥Ê‘⁄£¨«Û≥ˆµ„Pµƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£ª
£®4£©æÿ–ŒABCD≤ª∂Ø£¨Ω´≈◊ŒÔœþœÚ”“∆Ω“∆£¨µ±∆Ω“∆∫Ûµƒ≈◊ŒÔœþ”Îæÿ–Œµƒ±þ”–¡Ω∏ˆΩªµ„K°¢L£¨«“÷±œþKL∆Ω∑÷æÿ–Œµƒ√ʪ˝ ±£¨«Û≈◊ŒÔœþ∆Ω“∆µƒæý¿Î.
°æ¥∞∏°ø£®1£©y£Ω![]() x2©Å4x£ª£®2£©Àƒ±þ–ŒMNGF÷Ð≥§◊Ó–°÷µŒ™12
x2©Å4x£ª£®2£©Àƒ±þ–ŒMNGF÷Ð≥§◊Ó–°÷µŒ™12![]() £ª£®3£©¥Ê‘⁄µ„P£¨P◊¯±ÍŒ™£®6£¨©Å6£©£ª£®4£©≈◊ŒÔœþ∆Ω“∆µƒæý¿ÎŒ™3∏ˆµ•Œª≥§∂».
£ª£®3£©¥Ê‘⁄µ„P£¨P◊¯±ÍŒ™£®6£¨©Å6£©£ª£®4£©≈◊ŒÔœþ∆Ω“∆µƒæý¿ÎŒ™3∏ˆµ•Œª≥§∂».
°æΩ‚Œˆ°ø
£®1£©”…µ„E‘⁄x÷·’˝∞Î÷·«“µ„A‘⁄œþ∂ŒOE…œµ√µΩµ„A‘⁄x÷·’˝∞Î÷·…œ£¨À˘“‘A£®2£¨0£©£ª”…OA£Ω2£¨«“OA£∫AD£Ω1£∫3µ√AD£Ω6.”…”⁄Àƒ±þ–ŒABCDŒ™æÿ–Œ£¨π ”–AD°ÕAB£¨À˘“‘µ„D‘⁄µ⁄ÀƒœÛœÞ£¨∫·◊¯±Í”ÎAµƒ∫·◊¯±ÍœýÕ¨£¨Ω¯∂¯µ√µΩµ„D◊¯±Í.”…≈◊ŒÔœþæ≠π˝µ„D°¢E£¨”√¥˝∂®œµ ˝∑®º¥«Û≥ˆ∆‰Ω‚Œˆ Ω£ª£®2£©ª≠≥ˆÀƒ±þ–ŒMNGF£¨”…”⁄µ„F°¢G∑÷±‘⁄x÷·°¢y÷·…œ‘À∂Ø£¨π ø…◊˜µ„Mπÿ”⁄x÷·µƒ∂‘≥∆µ„µ„M'£¨◊˜µ„Nπÿ”⁄y÷·µƒ∂‘≥∆µ„µ„N'£¨µ√FM£ΩFM'°¢GN£ΩGN'.“◊µ√µ±M'°¢F°¢G°¢N'‘⁄Õ¨“ª÷±œþ…œ ±N'G+GF+FM'£ΩM'N'◊Ó–°£¨π Àƒ±þ–ŒMNGF÷Ð≥§◊Ó–°÷µµ»”⁄MN+M'N'.∏˘æðæÿ–Œ–‘÷ °¢≈◊ŒÔœþœþ–‘÷ µ»Ãıº˛«Û≥ˆµ„M°¢M'°¢N°¢N'◊¯±Í£¨º¥«Ûµ√¥∞∏£ª£®3£©“ÚŒ™ODø…«Û£¨«““—÷™°˜ODP÷–OD±þ…œµƒ∏þ£¨π ø…«Û°˜ODPµƒ√ʪ˝.”÷“ÚŒ™°˜ODPµƒ√ʪ˝≥£πÊ«Û∑® «π˝µ„P◊˜PQ∆Ω––y÷·Ωª÷±œþOD”⁄µ„Q£¨∞—°˜ODP≤∑÷Œ™°˜OPQ”ΰ˜DPQµƒ∫ÕªÚ≤Ó¿¥º∆À„£¨π ¥Ê‘⁄µ»¡øπÿœµ.…˵„P◊¯±ÍŒ™t£¨”√t±Ì æPQµƒ≥§º¥ø…¡–∑Ω≥Ã.«Ûµ√tµƒ÷µ“™Ã÷¬€ «∑Ò¬˙◊„µ„P‘⁄x÷·œ¬∑ΩµƒÃıº˛£ª£®4£©”…KL∆Ω∑÷æÿ–ŒABCDµƒ√ʪ˝ø…µ√K‘⁄œþ∂ŒAB…œ°¢L‘⁄œþ∂ŒCD…œ£¨ª≠≥ˆ∆Ω“∆∫Ûµƒ≈◊ŒÔœþø…÷™£¨µ„K”…µ„O∆Ω“∆µ√µΩ£¨µ„L”…µ„D∆Ω“∆µ√µΩ£¨π ”–K£®m£¨0£©£¨L£®2+m£¨-6£©.“◊÷§KL∆Ω∑÷æÿ–Œ√ʪ˝ ±£¨KL“ª∂®æ≠π˝æÿ–Œµƒ÷––ƒH«“±ªH∆Ω∑÷£¨«Û≥ˆH◊¯±ÍŒ™£®4£¨©Å3£©£¨”…÷–µ„◊¯±Íπ´ Ωº¥«Ûµ√mµƒ÷µ.
£®1£©°þµ„A‘⁄œþ∂ŒOE…œ£¨E£®8£¨0£©£¨OA£Ω2
°ýA£®2£¨0£©
°þOA£∫AD£Ω1£∫3
°ýAD£Ω3OA£Ω6
°þÀƒ±þ–ŒABCD «æÿ–Œ
°ýAD°ÕAB
°ýD£®2£¨©Å6£©
°þ≈◊ŒÔœþy£Ωax2+bxæ≠π˝µ„D°¢E
°ý![]()
Ω‚µ√£∫
°ý≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™y£Ω![]() x2©Å4x
x2©Å4x
£®2£©»ÁÕº1£¨◊˜µ„Mπÿ”⁄x÷·µƒ∂‘≥∆µ„M'£¨◊˜µ„Nπÿ”⁄y÷·µƒ∂‘≥∆µ„N'£¨¡¨Ω”FM'°¢GN'°¢M'N'
°þy£Ω![]() x2©Å4x£Ω
x2©Å4x£Ω![]() £®x©Å4£©2©Å8
£®x©Å4£©2©Å8
°ý≈◊ŒÔœþ∂‘≥∆÷·Œ™÷±œþx£Ω4
°þµ„C°¢D‘⁄≈◊ŒÔœþ…œ£¨«“CD°Œx÷·£¨D£®2£¨©Å6£©
°ýyC£ΩyD£Ω©Å6£¨º¥µ„C°¢Dπÿ”⁄÷±œþx£Ω4∂‘≥∆
°ýxC£Ω4+£®4©ÅxD£©£Ω4+4©Å2£Ω6£¨º¥C£®6£¨©Å6£©
°ýAB£ΩCD£Ω4£¨B£®6£¨0£©
°þAM∆Ω∑÷°œBAD£¨°œBAD£Ω°œABM£Ω90°„
°ý°œBAM£Ω45°„
°ýBM£ΩAB£Ω4
°ýM£®6£¨©Å4£©
°þµ„M°¢M'πÿ”⁄x÷·∂‘≥∆£¨µ„F‘⁄x÷·…œ
°ýM'£®6£¨4£©£¨FM£ΩFM'
°þNŒ™CD÷–µ„
°ýN£®4£¨©Å6£©
°þµ„N°¢N'πÿ”⁄y÷·∂‘≥∆£¨µ„G‘⁄y÷·…œ
°ýN'£®©Å4£¨©Å6£©£¨GN£ΩGN'
°ýCÀƒ±þ–ŒMNGF£ΩMN+NG+GF+FM£ΩMN+N'G+GF+FM'
°þµ±M'°¢F°¢G°¢N'‘⁄Õ¨“ª÷±œþ…œ ±£¨N'G+GF+FM'£ΩM'N'◊Ó–°
°ýCÀƒ±þ–ŒMNGF£ΩMN+M'N'=![]()
°ýÀƒ±þ–ŒMNGF÷Ð≥§◊Ó–°÷µŒ™12![]() .
.

£®3£©¥Ê‘⁄µ„P£¨ π°˜ODP÷–OD±þ…œµƒ∏þŒ™![]() .
.
π˝µ„P◊˜PQ°Œy÷·Ωª÷±œþOD”⁄µ„Q
°þD£®2£¨©Å6£©
°ýOD£Ω![]() £¨÷±œþODΩ‚Œˆ ΩŒ™y£Ω©Å3x
£¨÷±œþODΩ‚Œˆ ΩŒ™y£Ω©Å3x
…˵„P◊¯±ÍŒ™£®t£¨![]() t2©Å4t£©£®0£ºt£º8£©£¨‘Úµ„Q£®t£¨©Å3t£©
t2©Å4t£©£®0£ºt£º8£©£¨‘Úµ„Q£®t£¨©Å3t£©
¢Ÿ»ÁÕº2£¨µ±0£ºt£º2 ±£¨µ„P‘⁄µ„D◊Û≤ý
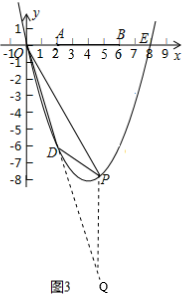
°ýPQ£ΩyQ©ÅyP£Ω©Å3t©Å£®![]() t2©Å4t£©£Ω©Å
t2©Å4t£©£Ω©Å![]() t2+t
t2+t
°ýS°˜ODP£ΩS°˜OPQ+S°˜DPQ£Ω![]() PQxP+
PQxP+![]() PQ£®xD©ÅxP£©£Ω
PQ£®xD©ÅxP£©£Ω![]() PQ£®xP+xD©ÅxP£©£Ω
PQ£®xP+xD©ÅxP£©£Ω![]() PQxD£ΩPQ£Ω©Å
PQxD£ΩPQ£Ω©Å![]() t2+t
t2+t
°þ°˜ODP÷–OD±þ…œµƒ∏þh£Ω![]() £¨
£¨
°ýS°˜ODP£Ω![]() ODh
ODh
°ý©Å![]() t2+t£Ω
t2+t£Ω![]() °¡2
°¡2![]() °¡
°¡![]()
∑Ω≥ÃŒÞΩ‚
¢⁄»ÁÕº3£¨µ±2£ºt£º8 ±£¨µ„P‘⁄µ„D”“≤ý
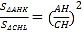
°ýPQ£ΩyP©ÅyQ£Ω![]() t2©Å4t©Å£®©Å3t£©£Ω
t2©Å4t©Å£®©Å3t£©£Ω![]() t2©Åt
t2©Åt
°ýS°˜ODP£ΩS°˜OPQ©ÅS°˜DPQ£Ω![]() PQxP©Å
PQxP©Å![]() PQ£®xP©ÅxD£©£Ω
PQ£®xP©ÅxD£©£Ω![]() PQ£®xP©ÅxP+xD£©£Ω
PQ£®xP©ÅxP+xD£©£Ω![]() PQxD£ΩPQ£Ω
PQxD£ΩPQ£Ω![]() t2©Åt
t2©Åt
°ý![]() t2©Åt£Ω
t2©Åt£Ω![]() °¡2
°¡2![]() °¡
°¡![]()
Ω‚µ√£∫t1£Ω©Å4£®…·»•£©£¨t2£Ω6
°ýP£®6£¨©Å6£©
◊€…œÀ˘ ˆ£¨µ„P◊¯±ÍŒ™£®6£¨©Å6£©¬˙◊„ π°˜ODP÷–OD±þ…œµƒ∏þŒ™![]() .
.
£®4£©…Ë≈◊ŒÔœþœÚ”“∆Ω“∆m∏ˆµ•Œª≥§∂»∫Û”Îæÿ–ŒABCD”–Ωªµ„K°¢L
°þKL∆Ω∑÷æÿ–ŒABCDµƒ√ʪ˝
°ýK‘⁄œþ∂ŒAB…œ£¨L‘⁄œþ∂ŒCD…œ£¨»ÁÕº4
°ýK£®m£¨0£©£¨L£®2+m£¨-6£©
¡¨Ω”AC£¨ΩªKL”⁄µ„H
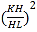
°þS°˜ACD£ΩSÀƒ±þ–ŒADLK£Ω![]() span>Sæÿ–ŒABCD
span>Sæÿ–ŒABCD
°ýS°˜AHK£ΩS°˜CHL
°þAK°ŒLC
°ý°˜AHK°◊°˜CHL
°ý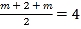 =
=![]() =1£¨
=1£¨
°ýAH£ΩCH£¨KH=HL£¨º¥µ„HŒ™AC÷–µ„£¨“≤ «KL÷–µ„
°ýH£®4£¨©Å3£©
°ý![]()
°ým£Ω3
°ý≈◊ŒÔœþ∆Ω“∆µƒæý¿ÎŒ™3∏ˆµ•Œª≥§∂».


 √˚–£øŒÃ√œµ¡–¥∞∏
√˚–£øŒÃ√œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
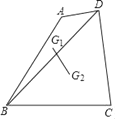
°æƒø°ø»ÁÕº£¨BD «Àƒ±þ–ŒABCDµƒ∂‘Ω«œþ£¨AB£ΩBC£Ω6£¨°œABC£Ω60°„£¨µ„G1°¢G2∑÷± «°˜ABD∫Õ°˜DBCµƒ÷ÿ–ƒ£¨‘Úµ„G1°¢G2º‰µƒæý¿ÎŒ™_____£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨µ»±þ°˜ABCµƒ±þ≥§Œ™2£¨µ„D «…‰œþBC…œµƒ“ª∏ˆ∂ص„£¨“‘ADŒ™±þœÚ”“◊˜µ»±þ°˜ADE£¨¡¨Ω·CE£¨
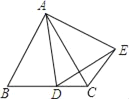
£®1£©«Û÷§£∫°˜ABD°’°˜ACE£ª
£®2£©»ÙCE£Ω![]() £¨«Û°˜ACDµƒ√ʪ˝£ª
£¨«Û°˜ACDµƒ√ʪ˝£ª
£®3£©»Ù°˜ACE «÷±Ω«»˝Ω«–Œ£¨‘ÚBDµƒ≥§ «°° °°£®÷±Ω”–¥≥ˆ¥∞∏£©£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øæð°∂÷–π˙ΩÔ˝±®°∑2004ƒÍ5‘¬24»’±®µ¿£∫ƒø«∞»´π˙”–Ω¸3ÕÚÀ˘÷––°—ßΩ®…Ë¡À–£‘∞Õ¯£¨∏√±®Œ™¡À¡ÀΩ‚’‚Ω¸3ÕÚÀ˘÷––°—ß–£‘∞Õ¯µƒΩ®…Ë«Èøˆ£¨¥”÷–≥È»°¡À4600À˘—ß–££¨∂‘’‚–©—ß–£–£‘∞Õ¯µƒΩ®…Ë«ÈøˆΩ¯––Œ æ̵˜≤È£¨≤¢∏˘æð¥æ̪Ê÷∆¡À»ÁÕºµƒ¡Ω∏ˆÕ≥º∆Õº£∫
Àµ√˜£∫Õ≥º∆Õº1µƒ∞Ÿ∑÷ ˝£Ω![]() °¡100%£ª
°¡100%£ª
Õ≥º∆Õº2µƒ∞Ÿ∑÷ ˝£Ω![]() °¡100%£Æ
°¡100%£Æ
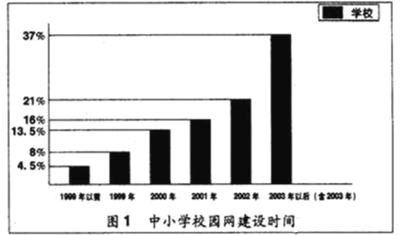
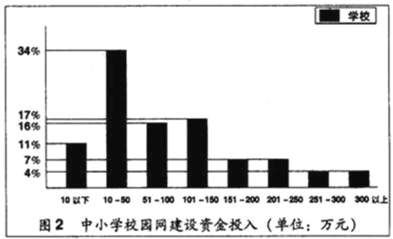
∏˘æð…œ√ʵƒŒƒ◊÷∫ÕÕ≥º∆ÕºÃ·π©µƒ–≈œ¢ªÿ¥œ¬¡–Œ £∫
£®1£©‘⁄’‚∏ˆŒ Â÷–£¨◊ÐÃÂ÷∏ ≤√¥£ø—˘±æ»ð¡ø « ≤√¥£ø
£®2£©π¿º∆£∫‘⁄»´π˙“—Ω®…Ë–£‘∞Õ¯µƒ÷––°—ß÷–£∫
¢Ÿ–£‘∞Õ¯Ω®…Ë ±º‰‘⁄2003ƒÍ“‘∫Û£®∫¨2003ƒÍ£©µƒ—ß–£¥Û‘º”–∂ý…ŸÀ˘£ø
¢⁄–£‘∞Õ¯Ω®…Ë◊ ΩÕ∂»Î‘⁄200ÕÚ‘™“‘…œ£®≤ª∫¨200ÕÚ‘™£©µƒ—ß–£¥Û‘º”–∂ý…ŸÀ˘£ø
£®3£©À˘≥È»°µƒ4600À˘—ß–£÷–£¨–£‘∞Õ¯Ω®…Ë◊ ΩÕ∂»Îµƒ÷–Œª ˝¬‰‘⁄ƒ«∏ˆ◊ Ω∂Œƒ⁄£ø
£®4£©Õº÷–ªπ÷π©¡À∆‰À˚–≈œ¢£¨¿˝»Á£∫–£‘∞Õ¯Ω®…Ë◊ ΩÕ∂»Î‘⁄10°´50ÕÚ‘™µƒ÷––°—ßµƒ ˝¡ø◊Ó∂ýµ»£¨«Î‘Ÿ–¥≥ˆ∆‰À˚¡ΩÃı–≈œ¢£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øœ÷»ÁΩÒ£¨°∞¿¨ª¯∑÷¿ý°±“‚ ∂“—…ӻλÀ–ƒ£¨¿¨ª¯“ª∞„ø…∑÷Œ™£∫ø…ªÿ ’ŒÔ°¢≥¯”ý¿¨ª¯°¢”–∫¶¿¨ª¯°¢∆‰À¸¿¨ª¯£Æ∆‰÷–º◊ƒ√¡À“ª¥¸¿¨ª¯£¨““ƒ√¡À¡Ω¥¸¿¨ª¯£Æ
£®1£©÷±Ω”–¥≥ˆº◊À˘ƒ√µƒ¿¨ª¯«°∫√ «°∞≥¯”ý¿¨ª¯°±µƒ∏≈¬ £ª
£®2£©«Û““À˘ƒ√µƒ¡Ω¥¸¿¨ª¯≤ªÕ¨¿ýµƒ∏≈¬ .
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø2013ƒÍ3‘¬£¨ƒ≥√∫øÛ∑¢…˙ÕþÀ𱨒®£¨∏√µÿ滑Æ∂”¡¢º¥∏œ∏∞œ÷≥°Ω¯––滑ƣ¨æ»‘Æ∂”¿˚”√…˙√¸ÃΩ≤‚“«‘⁄µÿ√ÊA°¢B¡Ω∏ˆÃΩ≤‚µ„ÃΩ≤‚µΩC¥¶”–…˙√¸º£œÛ£Æ“—÷™A°¢B¡Ωµ„œýæý4√◊£¨ÃΩ≤‚œþ”εÿ√ʵƒº–Ω«∑÷± «30°„∫Õ45°„£¨ ‘»∑∂®…˙√¸À˘‘⁄µ„Cµƒ…Ó∂»£Æ£®æ´»∑µΩ0.1√◊£¨≤Œøº ˝æð£∫![]() £©
£©
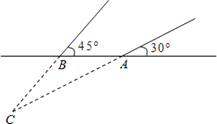
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±ÍœµxOy÷–£¨”–“ª∏ˆ”…¡˘∏ˆ±þ≥§Œ™1µƒ’˝∑Ω–Œ◊È≥…µƒÕº∞∏£¨∆‰÷–µ„A£¨Bµƒ◊¯±Í∑÷±Œ™(3,5)£¨(6,1)£Æ»Ùπ˝‘≠µ„µƒ÷±œþlΩ´’‚∏ˆÕº∞∏∑÷≥…√ʪ˝œýµ»µƒ¡Ω≤ø∑÷£¨‘Ú÷±œþlµƒ∫Ø ˝Ω‚Œˆ ΩŒ™_____£Æ
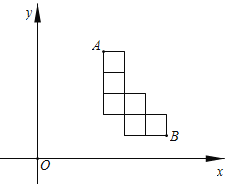
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨∆Ω––Àƒ±þ–ŒABCD÷–£¨E£¨F∑÷±Œ™AD£¨BC±þ…œµƒ“ªµ„£¨‘ˆº”œ¬¡–Ãıº˛£¨≤ªƒÐµ√≥ˆBE°ŒDFµƒ «£®°°°°£©

A. AE=CF B. BE=DF C. °œEBF=°œFDE D. °œBED=°œBFD
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø”√A°¢B¡Ω÷÷ª˙∆˜»À∞·‘À¥Û√◊£¨A–Õª˙∆˜»À±»B–Õª˙∆˜»À√ø–° ±∂ý∞·‘À20¥¸¥Û√◊£¨A–Õª˙∆˜»À∞·‘À700¥¸¥Û√◊”ÎB–Õª˙∆˜»À∞·‘À500¥¸¥Û√◊À˘”√ ±º‰œýµ»£Æ«ÛA°¢B–Õª˙∆˜»À√ø–° ±∑÷±∞·‘À∂ý…Ÿ¥¸¥Û√◊£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com