
����Ŀ��ij��ѧΪ��������У���ƻ������ס������ֹ����������¹�����ͼ�飬���鷢�֣�������������3�����������2���������ʽ�1020Ԫ��������������4�����������3���������ʽ�1440Ԫ��
��1���ס����������ÿ���ļ۸�ֱ��Ƕ���Ԫ��
��2������У�ƻ����������ֹ������20�������������������������ڼ�������������ѧУ�����ܹ��ṩ�ʽ�4320Ԫ������Ƽ��ֹ��������ѧУѡ��
���𰸡���1����������Ϊ180Ԫ���������ĵ���Ϊ240Ԫ����2��ѧУ�Ĺ������������֣�����һ���������8�����������12�����������������9�����������11�������������������10�����������10����
��������
��1����������ΪxԪ���������ĵ���ΪyԪ�����ݣ�������������3�����������2���������ʽ�1020Ԫ��������������4�����������3���������ʽ�1440Ԫ�г�������⼴�ɣ�
��2������������m���������������20-m���������ݣ����辭��=��ͼ����ܷ���+��ͼ����ܷ��á��ܾ���W��1820,�ҹ���ļ���ͼ��������������ͼ��������г�����ʽ�飬�ⲻ��ʽ�鼴�ɵIJ���ʽ��Ľ⼯���Ӷ�ȷ��������
��1���⣺��������ΪxԪ���������ĵ���ΪyԪ��������ã�
![]() ��
��
��ã�![]() ��
��
����������Ϊ180Ԫ���������ĵ���Ϊ240Ԫ��
��2���⣺����������m���������������20-m������
������ã�![]()
��ã�8��m��10
��Ϊmȡ����������m����ȡ��ֵΪ��8��9��10
����ѧУ�Ĺ������������֣�
����һ���������8�����������12����
���������������9�����������11����
���������������10�����������10����


 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
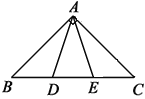
����Ŀ����ͼ������ABC�У� ��BAC=90�㣬 AB=AC=2![]() ����D��E���ڱ�BC�ϣ�����DAE=45������BD=1����DE=__________��
����D��E���ڱ�BC�ϣ�����DAE=45������BD=1����DE=__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
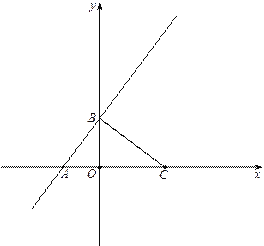
����Ŀ����ͼ����֪A��n����2����B��1��4����һ�κ���y=kx+b��ͼ��ͷ���������y=![]() ��ͼ����������㣬ֱ��AB��y�ύ�ڵ�C��
��ͼ����������㣬ֱ��AB��y�ύ�ڵ�C��
��1������������һ�κ����Ĺ�ϵʽ��
��2�����AOC�������
��3����ʽkx+b��![]() ��0�Ľ⼯����ֱ��д���𰸣�
��0�Ľ⼯����ֱ��д���𰸣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˼�ǿѧ���İ�ȫ��ʶ��ijУ��֯��ѧ���μӰ�ȫ֪ʶ���������г�ȡ�˲���ѧ���ɼ����÷���ȡ������������Ϊ100�֣�����ͳ�ƣ���֪A���Ƶ��a��B���Ƶ��bС24������ͳ��Ƶ���ֲ�ֱ��ͼ��δ��ɣ�������ͼ���£������������⣺
��1����������Ϊ��______��aΪ______��
��2��nΪ________��E����ռ����Ϊ________��
��3����ȫƵ���ֲ�ֱ��ͼ��
��4�����ɼ���80�����ϼ������㣬ȫУ����2000��ѧ�������Ƴɼ�����ѧ����_________����


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=��x+b��˫���� ![]() ��x��0������A��B���㣬��x�ᡢy��ֱ���E��F���㣬����OA��OB����S��AOB=S��OBF+S��OAE �� ��b= ��
��x��0������A��B���㣬��x�ᡢy��ֱ���E��F���㣬����OA��OB����S��AOB=S��OBF+S��OAE �� ��b= �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���C������Ϊ��4��0����һ�κ���![]() ��ͼ��ֱ�x�ᡢy���ڵ�A����B.
��ͼ��ֱ�x�ᡢy���ڵ�A����B.
�� ����D��ֱ��AB�ڵ�һ�����ڵĵ㣬��BD��BC���������D������.
�� �ڢŵ������£�����Q���������ϵ�һ�����㣬��̽���ڵ�һ�����Ƿ������һ����P��ʹ����B��D��P��QΪ������ı�����������BDΪ���ε�һ�ߣ��������ڣ���ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ������������AB��CD��ˮƽ����Ϊ30m������ͬѧס�ڽ�����AB��10¥P�ң����۲⽨����CD¥�Ķ���D��������Ϊ30�㣬��õײ�C���ĸ���Ϊ45�㣬������CD�ĸ߶ȣ��� ![]() ȡ1.73�����������������
ȡ1.73�����������������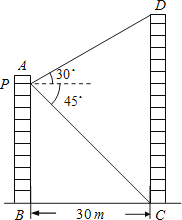
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���ABCD�����������ֱ�ΪA(0,1)��B(5,1)��C(7,3)��D(2,5).

(1)����ͼ��ʾ��ƽ��ֱ������ϵ�������ı��Σ�
(2)�ı���ABCD�������________��
(3)�ı���ABCD�ڣ��߽�����)һ����_____������(��������������궼�������ĵ�).
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com