
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边上的中点,
边上的中点,![]() 于点
于点![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() ;
;
(2)求证:![]() 垂直平分
垂直平分![]() .
.

【答案】(1)见详解;(2)见详解
【解析】
(1)根据ASA判定△ACD≌△CBF即可;
(2)由(1)得到BF=CD,由D为BC中点,根据中点定义得到CD=BD,等量代换得到BF=BD,再根据角度之间的数量关系求出∠ABC=∠ABF,即BA是∠FBD的平分线,从而利用等腰三角形三线合一的性质求证即可.
解:(1)∵∠BCE+∠ACE=90°,∠ACE+∠CAE=90°,
∴∠BCE=∠CAE.
∵AC⊥BC,BF∥AC.
∴BF⊥BC.
∴∠ACD=∠CBF=90°,
∵AC=CB,
∴△ACD≌△CBF;
(2)连接DF,
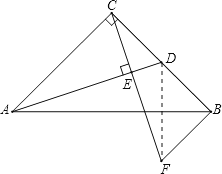
由(1)得CD=BF
∵![]() 为
为![]() 边上的中点
边上的中点
∴CD=BD=![]() BC
BC
∴BF=BD
∴△BFD为等腰直角三角形
∵∠ACB=90°,CA=CB,
∴∠ABC=45°.
∵∠FBD=90°,
∴∠ABF=45°.
∴∠ABC=∠ABF,即BA是∠FBD的平分线.
∴根据等腰三角形三线合一的性质有BA⊥FD,BA平分边FD,
即AB垂直平分DF.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A(0,1),点B(3,0),点C(4,3).
(1)判断△ABC的形状并说明理由;
(2)在线段OC的右侧,以OC为边作等腰直角△OCD,点D的坐标为 .
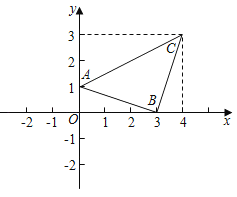
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A,B两地同时相向匀速行驶,当乙车到达A地后,继续保持原速向远离B的方向行驶,而甲车到达B地后立即掉头,并保持原速与乙车同向行驶,经过15小时后两车同时到达距A地300千米的C地(中途休息时间忽略不计).设两车行驶的时间为x(小时),两车之间的距离为y(千米),y与x之间的函数关系如图所示,则当甲车到达B地时,乙车距A地_____千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,放在直角坐标系中的正方形ABCD边长为4,现做如下实验:抛掷一枚均匀的正四面体骰子(它有四个顶点,各顶点的点数分别是1至4这四个数字中一个),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的顶点数作为直角坐标中P点的坐标)第一次的点数作横坐标,第二次的点数作纵坐标).
(1)求P点落在正方形ABCD面上(含正方形内部和边界)的概率.
(2)将正方形ABCD平移整数个单位,则是否存在一种平移,使点P落在正方形ABCD
面上的概率为0.75;若存在,指出其中的一种平移方式;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,∠A=30°,AC=2.将△ABC绕点C顺时针旋转120°得△A′B′C.
(1)求作:△A′B′C;
(2)求点B旋转经过的路径长;
(3)求线段BB′的长;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在下列条件中,不能作为判断△ABD≌△BAC的条件是( )

A. ∠D=∠C,∠BAD=∠ABC B. ∠BAD=∠ABC,∠ABD=∠BAC
C. BD=AC,∠BAD=∠ABC D. AD=BC,BD=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点.将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.
 试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2018双十一购物狂欢节”,京东商城当天的交易额约1600亿元.“预计在2020双十一购物狂欢节”京东商城当天的交易额能达到约1936亿元.
(1)求出2018至2020年京东商城双十一当天的交易额的年平均增长率;
(2)刘老师在“双十一”到来之前,分别在京东商城的两家店里选了一套标价为1900元的书籍和一件标价为990元的羽绒服.据了解,双十一当天书籍打五五折后再降价![]() n%.同时,该羽绒服店的老板先将羽绒服提价
n%.同时,该羽绒服店的老板先将羽绒服提价![]() n%,双十一当天再降价
n%,双十一当天再降价![]() n%,最后刘老师双十一购买两种商品所花费的总金额恰好是1760元.求n的值.
n%,最后刘老师双十一购买两种商品所花费的总金额恰好是1760元.求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节前小明花1200元从市场购进批发价分别为每箱30元与50元的![]() 、
、![]() 两种水果进行销售,分别以每箱35元与60元的价格出售,设购进
两种水果进行销售,分别以每箱35元与60元的价格出售,设购进![]() 水果
水果![]() 箱,
箱,![]() 水果
水果![]() 箱.
箱.
(1)求![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)若要求购进![]() 水果的数量不少于
水果的数量不少于![]() 水果的数量,则应该如何分配购进
水果的数量,则应该如何分配购进![]() 、
、![]() 水果的数量并全部售出才能获得最大利润,此时最大利润是多少?
水果的数量并全部售出才能获得最大利润,此时最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com