练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．在平面直角坐标系中，线段A′B′是由线段AB经过平移得到的，已知点A（-2，1）的对应点为A′（3，-1），点B的对应点为B′（4，0），则点B的坐标为（　　）
    A．（9，-2）B．（-1，-2）C．（9，2）D．（-1，2）

    分析 直接利用平移中点的变化规律求解即可．

    解答 解：横坐标从-2到3，说明是向右移动了3-（-2）=5，纵坐标从1到-1，说明是向下移动了1-（-1）=2，
    求原来点的坐标，则为让新坐标的横坐标都减5，纵坐标都加2．
    则点B的坐标为（-1，2）．
    故选D．

    点评 本题考查了图形的平移变换，注意左右移动改变点的横坐标，左减，右加；上下移动改变点的纵坐标，下减，上加．求原来点的坐标正好相反．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

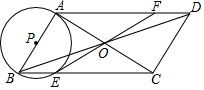    4．如图，在四边形ABCD中，对角线AC，BD相交于点O，且OA=OC，OB=OD，∠BAC=90°，以AB为直径的⊙P交BC于点E，连接EO并延长交AD于点F．
    （1）求证：OE是⊙P的切线；
    （2）OA=OF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．计算：$\sqrt{2}$×$\sqrt{8}$-（2-$\sqrt{3}$）0=3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．已知抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A，B两点，A点位于y轴左侧，B点位于A点右侧，且OA=2，与y轴相交于点C，OC=4，点P为抛物线上的任意一点，且在线段BC的上方．
    （1）求抛物线的解析式，并画出图形；
    （2）试求当P点运动到什么位置时，△PBC的面积最大并求其最大值；
    （3）在抛物线的对称轴上是否存在点Q，使得AQ=CQ？若存在，求出符合条件的Q点坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图，已知点E在正方形ABCD在内，AE=6，BE=8，AB=10，求图中阴影部分的面积S．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．如图，一次函数y=kx+1的图形经过点A（1，2），且与x轴相交于点B，若点P是y轴上一点，且满足△APB是等腰三角形，则点P的坐标可以是（0，2+$\sqrt{7}$），（0，2-$\sqrt{7}$），（0，$\sqrt{7}$），（0，-$\sqrt{7}$）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．已知不等式组$\left\{\begin{array}{l}{x+a≥-1}\\{b-x≥0}\end{array}\right.$的解集为-2≤x≤3，则b-a的值为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．完成下面的证明：
    如图，已知∠BAG与∠AGD互补，且∠1=∠2，求证：∠E=∠F．
    证明：∵∠BAG与∠AGD互补（已知）．
    ∴AB∥CD（同旁内角互补两直线平行）
    ∴∠BAG=∠AGC（两直线平行，内错角相等）
    又∵∠1=∠2（已知）
    ∴∠BAG-∠1=∠AGC-∠2（等式的性质）
    即∠3=∠4
    ∴AE∥FG（内错角相等，两直线平行）
    ∴∠E=∠F（两直线平行，内错角相等）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．在一个不透明的口袋里装有若干个相同的红球，为了用估计袋中红球的数量，八（1）班学生在数学实验室分组做摸球实验：每组先将10个与红球大小形状完全相同的白球装入袋中，搅匀后从中随机摸出一个球并记下颜色，再把它放回袋中，不断重复．下表是这次活动统计汇总各小组数据后获得的全班数据统计表：
    摸球的次数s15030060090012001500
    摸到白球的频数n63a247365484606
    摸到白球的频率$\frac{n}{s}$0.4200.4100.4120.4060.403b
    （1）按表格数据格式，表中的a=123；b=0.404；
    （2）请估计：当次数s很大时，摸到白球的频率将会接近0.4（精确到0.1）；
    （3）请推算：摸到红球的概率是0.6（精确到0.1）；
    （4）试估算：这一个不透明的口袋中红球有15只．

    查看答案和解析>>

    同步练习册答案