
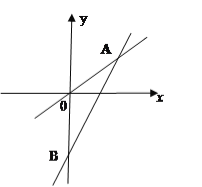
【题目】如图表示一个正比例函数与一个一次函数的图象,它们交于点A(4,3),其中一次函数的图象与y轴交于点B,且OA=OB,求这两个函数的解析式.
科目:初中数学 来源: 题型:
【题目】下列每一组数据中的三个数值分别为三角形的三边长,能构成直角三角形的是( )
A. 3,5,6 B. 2,4,5 C. 6,7,8 D. 1.5,2,2.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)(2015秋万州区期末)在△ABC中,AB=AC,BG⊥AC于G,DE⊥AB于E,DF⊥AC于F.
(1)如图1,若D是BC边上的中点,∠A=45°,DF=3,求AC的长;
(2)如图2,D是线段BC上的任意一点,求证:BG=DE+DF;
(3)在图3,D是线段BC延长线上的点,猜想DE、DF与BG的关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣2与x轴交于A、B两点,与y轴交于点C,已知A(﹣1,0),且tan∠ABC=![]() .
.
(1)求抛物线的解折式.
(2)在直线BC下方抛物线上一点P,当四边形OCPB的面积取得最大值时,求此时点P的坐标.
(3)在y轴的左侧抛物线上有一点M,满足∠MBA=∠ABC,若点N是直线BC上一点,当△MNB为等腰三角形时,求点N的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解我县七年级2000名学生的身高情况,从中抽取了200学生测量身高,在这个问题中,样本是( )
A. 200 B. 2000名学生 C. 200名学生的身高情况 D. 200名学生
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知线段AB、CD相交于点O,连接AC、BD,我们把形如图1的图形称之为“8字形”.如图2,∠CAB和∠BDC的平分线AP和DP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:
(1)仔细观察,在图2中有 个以线段AC为边的“8字形”;
(2)在图2中,若∠B=96°,∠C=100°,求∠P的度数.
(3)在图2中,若设∠C=α,∠B=β,∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB,试问∠P与∠D、∠B之间存在着怎样的数量关系(用α、β表示∠P),并说明理由;
∠CDB,试问∠P与∠D、∠B之间存在着怎样的数量关系(用α、β表示∠P),并说明理由;
(4)如图3,则∠A+∠B+∠C+∠D+∠E+∠F的度数为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算(﹣3x)(2x2﹣5x﹣1)的结果是( )
A.﹣6x2﹣15x2﹣3x
B.﹣6x3+15x2+3x
C.﹣6x3+15x2
D.﹣6x3+15x2﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中,是确定事件的是( )
A. 打开电视机,它正在播放广告
B. 明天一定是天晴
C. 任意掷一枚质地均匀的骰子,掷出的点数是奇数
D. 抛出的篮球会下落
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com