
 如图,一垂直于水平地面的灯柱AB被一钢筋CD固定,CD与地面成45°角(∠CDB=45°),在点C上方2m处加固另一条钢筋DE,DE与地面成60°角(∠EDB=60°),则钢筋DE的长度约为多少?(结果精确到0.1m,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,一垂直于水平地面的灯柱AB被一钢筋CD固定,CD与地面成45°角(∠CDB=45°),在点C上方2m处加固另一条钢筋DE,DE与地面成60°角(∠EDB=60°),则钢筋DE的长度约为多少?(结果精确到0.1m,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73) 分析 设BD=x米,则BC=x米,BE=(x+2)米,解Rt△BDE,得出BE=BD•tan∠EDB=$\sqrt{3}$x,根据BE不变列出方程$\sqrt{3}$x=x+2,求出x≈2.73,那么DE=$\frac{BD}{cos∠EDB}$=2BD,从而求得DE的长.
解答 解:设BD=x米,
∵在Rt△BDC中,∠CDB=45°,
∴BC=x米,BE=BC+CE=(x+2)米,
∵在Rt△BDE中,∠EDB=60°,
∴BE=BD•tan∠EDB=$\sqrt{3}$x,
∴$\sqrt{3}$x=x+2,
解得,x≈2.73,
∴DE=$\frac{BD}{cos∠EDB}$=2BD≈5.5.
即钢筋DE的长度约为5.5m.
点评 本题考查了解直角三角形的应用,解题的关键是明确题意,利用三角函数值求出相应的边的长度.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
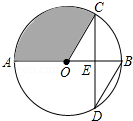 如图,AB是⊙O的直径,弦CD交AB于点E,且E为OB的中点,∠CDB=30°,CD=4$\sqrt{3}$,则阴影部分的面积$\frac{16}{3}$π.
如图,AB是⊙O的直径,弦CD交AB于点E,且E为OB的中点,∠CDB=30°,CD=4$\sqrt{3}$,则阴影部分的面积$\frac{16}{3}$π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
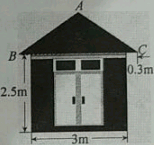 一个住宅区的配电房示意图如图所示,它是一个轴对称图形.已知∠ABC=35°,求配电房房顶离地面的高度(精确到0.1m).(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)
一个住宅区的配电房示意图如图所示,它是一个轴对称图形.已知∠ABC=35°,求配电房房顶离地面的高度(精确到0.1m).(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
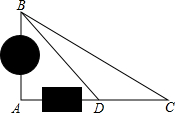 如图,是某社区的一个直角三角形的休闲广场,在直角边AB上修有一处养鱼池,直角边AC上有一个花坛.现测得∠C=30°,从点C沿CA方向前进50米到达点D,测得∠ADB=45°,请你计算AB及AC的长度.(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.73)
如图,是某社区的一个直角三角形的休闲广场,在直角边AB上修有一处养鱼池,直角边AC上有一个花坛.现测得∠C=30°,从点C沿CA方向前进50米到达点D,测得∠ADB=45°,请你计算AB及AC的长度.(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.73)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com