
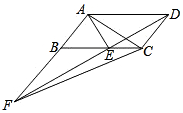
 如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:①△ABC≌△AED;②△ABE是等边三角形;③AD=AF;④S△ABE=S△CEF;⑤S△ABE=S△CDE.其中正确的是( )
如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:①△ABC≌△AED;②△ABE是等边三角形;③AD=AF;④S△ABE=S△CEF;⑤S△ABE=S△CDE.其中正确的是( )| A. | ①②③ | B. | ①②⑤ | C. | ①②④ | D. | ①③④ |
分析 由平行四边形的性质得出AD∥BC,AD=BC,由AE平分∠BAD,可得∠BAE=∠DAE,可得∠BAE=∠BEA,得AB=BE,由AB=AE,得到△ABE是等边三角形,②正确;则∠ABE=∠EAD=60°,由SAS证明△ABC≌△EAD,①正确;由△FCD与△ABD等底(AB=CD)等高(AB与CD间的距离相等),得出S△FCD=S△ABD,由△AEC与△DEC同底等高,所以S△AEC=S△DEC,得出S△ABE=S△CEF.④正确.
解答 解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠EAD=∠AEB,
又∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠BEA,
∴AB=BE,
∵AB=AE,
∴△ABE是等边三角形;
②正确;
∴∠ABE=∠EAD=60°,
∵AB=AE,BC=AD,
∴△ABC≌△EAD(SAS);
①正确;
∵△FCD与△ABC等底(AB=CD)等高(AB与CD间的距离相等),
∴S△FCD=S△ABC,
又∵△AEC与△DEC同底等高,
∴S△AEC=S△DEC,
∴S△ABE=S△CEF;④正确.
若AD与AF相等,即∠AFD=∠ADF=∠DEC
即EC=CD=BE
即BC=2CD,
题中未限定这一条件
∴③⑤不一定正确;
故选:C.
点评 此题考查了平行四边形的性质、等边三角形的判定与性质、全等三角形的判定与性质.此题比较复杂,注意将每个问题仔细分析.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:解答题
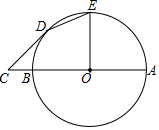 已知AB为⊙O的直径,C为AB延长线上一点,CD切⊙O于点D,CD=4,BC=2
已知AB为⊙O的直径,C为AB延长线上一点,CD切⊙O于点D,CD=4,BC=2查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,在?ABCD中,对角线AC,BC相交于点O,已知△BOC与△AOB的周长之差为4,?ABCD的周长为28,则BC的长度为( )
如图所示,在?ABCD中,对角线AC,BC相交于点O,已知△BOC与△AOB的周长之差为4,?ABCD的周长为28,则BC的长度为( )| A. | 5 | B. | 6 | C. | 7 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
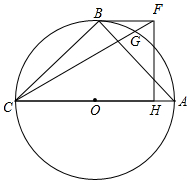 如图,△ABC内接于⊙O,AC是直径,BC=BA,在∠ACB的内部作∠ACF=30°,且CF=CA,过点F作FH⊥AC于点H,连接BF.
如图,△ABC内接于⊙O,AC是直径,BC=BA,在∠ACB的内部作∠ACF=30°,且CF=CA,过点F作FH⊥AC于点H,连接BF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 355<444<533 | B. | 444<355<533 | C. | 533<444<355 | D. | 533<355<444 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 若将三个数$\sqrt{3}$,3$\sqrt{2}$,2$\sqrt{3}$表示在数轴上,则能被如图所示的墨迹覆盖的数是$\sqrt{3}$.
若将三个数$\sqrt{3}$,3$\sqrt{2}$,2$\sqrt{3}$表示在数轴上,则能被如图所示的墨迹覆盖的数是$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6折 | B. | 7折 | C. | 8折 | D. | 9折 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com