
【题目】(1)请在横线上填写合适的内容,完成下面的证明:
如图①如果AB∥CD,求证:∠APC=∠A+∠C.
证明:过P作PM∥AB.
所以∠A=∠APM,( )
因为PM∥AB,AB∥CD(已知)
所以∠C= ( )
因为∠APC=∠APM+∠CPM
所以∠APC=∠A+∠C(等量代换)
(2)如图②,AB∥CD,根据上面的推理方法,直接写出∠A+∠P+∠Q+∠C= .
(3)如图③,AB∥CD,若∠ABP=x,∠BPQ=y,∠PQC=z,∠QCD=m,则m= (用x、y、z表示)

【答案】(1)见解析;(2)540°;(3)x﹣y+z.
【解析】
(1)根据平行线的性质可得;
(2)过点P作PM∥AB,过点Q作QN∥CD,将∠A、∠P、∠Q、∠C划分为6个3对同旁内角,由平行线的性质可得;
(3)延长PQ交CD于点E,延长QP交AB于点F,可得∠BFP=∠CEQ,根据三角形外角定理知∠BFP=∠BPQ-∠B、∠CEQ=∠PQC-∠C,整理后即可得.
(1)过P作PM∥AB,
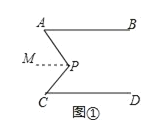
所以∠A=∠APM,(两直线平行,内错角相等)
因为 PM∥AB,AB∥CD (已知 )
所以 PM∥CD,
所以∠C=∠CPM,(两直线平行,内错角相等)
因为∠APC=∠APM+∠CPM
所以∠APC=∠A+∠C (等量代换 ),
故答案为:两直线平行,内错角相等;∠CPM;两直线平行,内错角相等.
(2)如图②,过点P作PM∥AB,过点Q作QN∥CD,
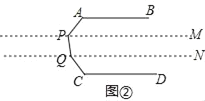
∴∠A+∠APM=180°,∠C+∠CQN=180°,
又∵AB∥CD,
∴PM∥QN,
∴∠MPQ+∠NQP=180°,
则∠A+∠APQ+∠CQP+∠C=∠A+∠APM+∠MPQ+∠NQP+∠CQN+∠C=540°,
故答案为:540°.
(3)如图③,延长PQ交CD于点E,延长QP交AB于点F,

∵AB∥CD,
∴∠BFP=∠CEQ,
又∵∠BPQ=∠BFP+∠B,∠PQC=∠CEQ+∠C,
即∠BFP=∠BPQ﹣∠B,∠CEQ=∠PQC﹣∠C,
∴∠BPQ﹣∠B=∠PQC﹣∠C,即y﹣x=z﹣m,
∴m=x﹣y+z,
故答案为:x﹣y+z.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】若将一幅三角板按如图所示的方式放置,则下列结论中不正确的是( )

A. ∠1=∠3 B. 如果∠2=30°,则有AC∥DE
C. 如果∠2=30°,则有BC∥AD D. 如果∠2=30°,必有∠4=∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 经过第一、二、三象限,与
经过第一、二、三象限,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 在这条直线上,连接
在这条直线上,连接![]() ,已知
,已知![]() 的面积等于1.
的面积等于1.

(1)求![]() 的值;
的值;
(2)如果反比例函数y=![]() (k是常量,k≠0)的图象经过点A,求这个反比例函数的解析式。
(k是常量,k≠0)的图象经过点A,求这个反比例函数的解析式。
查看答案和解析>>
科目:初中数学 来源: 题型:
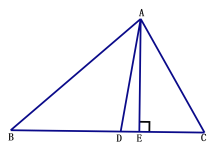
【题目】如图,AD、AE分别是△ABC的角平分线和高线.
(1) 若∠B=50°,∠C=60°,求∠DAE的度数;
(2)若∠C >∠B,猜想∠DAE与∠C-∠B之间的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O,A在数轴上表示的数分别是0,l,将线段OA分成1000等份,其分点由左向右依次为M1,M2…M999;将线段OM1分成1000等份,其分点由左向右依次为N1,N2…N999;将线段ON1分成1000等份,其分点由左向右依次为P1,P2…P999.则点P314所表示的数用科学记数法表示为_____.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形.
(2)平移△ABC,使点A的对应点A2坐标为(-2,-6),请画出平移后对应的△A2B2C2的图形.
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上,请解答下列问题
(1)画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1,并写出点C1的坐标;
(2)画出将△ABC关于原点O对称的图形△A2B2C2,并写出点C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某庄有甲、乙两家草莓采摘园的草莓销售价格相同,春节期间,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为![]() (千克),在甲园所需总费用为
(千克),在甲园所需总费用为![]() (元),在乙园所需总费用为
(元),在乙园所需总费用为![]() (元),
(元),![]() 、
、![]() 与
与![]() 之间的函数关系如图所示.
之间的函数关系如图所示.
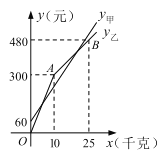
(1)甲采摘园的门票是_____元,两个采摘园优惠前的草莓单价是每千克____元;
(2)当![]() 时,求
时,求![]() 与
与![]() 的函数表达式;
的函数表达式;
(3)游客在“春节期间”采摘多少千克草莓时,甲、乙两家采摘园的总费用相同.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com