
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),其对称轴为直线x=1,下列结论中正确的是( )
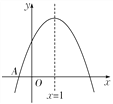
A. abc>0 B. 2a-b=0 C. 4a+2b+c<0 D. 9a+3b+c=0
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,
,![]() ,且点
,且点![]() 的坐标为
的坐标为![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
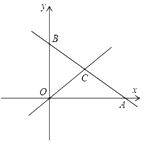
(1)点![]() 的坐标是________,点
的坐标是________,点![]() 的坐标是________;
的坐标是________;
(2)直线![]() 上有一点
上有一点![]() ,若
,若![]() ,试求出点
,试求出点![]() 的坐标;
的坐标;
(3)若点![]() 为直线
为直线![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的垂线,与直线
轴的垂线,与直线![]() 交于点
交于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长度为
的长度为![]() ,求
,求![]() 与
与![]() 的函数解析式.
的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在阳光下,小东测得一根长为1 m的竹竿的影长为0.4 m.
(1)求同一时刻2 m的竹竿的影长;
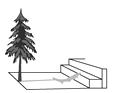
(2)同一时刻小东在测量树的高度时,发现树的影子不全落在地面上,有一部分落在操场的第一级台阶上,如图,测得落在第一级台阶上的影子长为0.1 m,第一级台阶的高为0.3 m,落在地面上的影子长为4.3 m,求树的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中,点P是边AD上的动点(点P不与点A、点D重合),点Q是边CD上一点,连接PB、PQ,且∠PBC=∠BPQ.
⑴ 若tan∠PBC=4,求AP的长;
⑵ 是否存在点P,使得点Q恰好是边CD的中点?若存在,求出AP的长;若不存在,请说明理由.⑶ 连接BQ,在△PBQ中是否存在度数不变的角?若存在,指出这个角,并求出它的度数;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0 ②4a+2b+c>0 ③4ac﹣b2<8a ④![]() <a<
<a<![]() ⑤b>c.其中含所有正确结论的选项是( )
⑤b>c.其中含所有正确结论的选项是( )

A. ①③ B. ①③④ C. ②④⑤ D. ①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】① 如图(1),直线l上有2个点,则图中有2条可用图中字母表示的射线:A1A2、A2A1,有1条线段:A1A2;
② 如图(2),直线l上有3个点,则图中有几条可用图中字母表示的射线,有几条线段,并分别用图中字母表示出来;
③ 如图(3),直线l上有n个点,则图中有多少条可用图中字母表示的射线,有多少条线段,分别用含n的代数式表示出来;
④ 应用(3)中发现的规律解决问题:某校七年级共有8个班进行足球比赛,准备进行循环赛(即每两队之间赛一场),预计全部赛完共需多少场比赛?
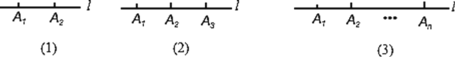
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东方小商品市场一经营者将每件进价为80元的某种小商品原来按每件100元出售,一天可售出100件.后来经过市场调查,发现这种小商品单价每降低1元,其销量可增加10件.
(1)该经营者经营这种商品原来一天可获利润____元;
(2)若设后来该小商品每件降价x元,该经营者一天可获利润y元.
①若该经营者经营该商品一天要获利润2 090元,求每件商品应降价多少元?
②求出y与x之间的函数关系式,并求出当x取何值时,该经营者所获利润最大,且最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
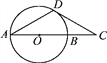
【题目】如图所示,D是半径为R的⊙O上一点,过点D作⊙O的切线交直径AB的延长线于点C,下列四个条件:①AD=CD;②∠A=30°;③∠ADC=120°;④DC=![]() R.其中能使得BC=R的有________(填序号).
R.其中能使得BC=R的有________(填序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com