
【题目】如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片,点A在x轴上,点C在y轴上,将边BC折叠,使点B落在OA上的点D处,已知折痕CE=5![]() ,且4AE=3AD.
,且4AE=3AD.
①判断△OCD与△ADE是否相似,请说明理由。
②求直线CE与x轴的交点P的坐标。
③是否存在过点D的直线l,使直线l与两坐标轴围成的三角形与直线CE与两坐标轴围成的三角形相似,如果存在,请求出其解析式,如果不存在,请说明理由。

【答案】①相似,证明详见解析;②P(16,0);③存在,![]() ;
;![]() ;y=-2x+12;
;y=-2x+12;![]()
【解析】
(1)运用同角的余角相等得到∠CDO=∠DEA即可证明相似,
(2)由△OCD∽△ADE求出OA,OD之间的关系,再在直角三角形CBE中勾股定理即可解题,
(3)分情况讨论,当△ODM∽△OPC时和当△OMD∽△OPC由比例式得到M的坐标即可求解.
解:①由对称性得∠CDE=∠B=90°
∴∠CDO+∠EDA=90°
∴∠CDO=∠DEA
∵∠COD=∠DAE=90°
∴△OCD∽△ADE
②设AE=3x
∵tan∠EDA=![]()
∴AD=4x,DE=5x
∴AB=8x=OC
∵由△OCD∽△ADE
∴![]()
∴OD=6x
∴OA=10x
∵CE2=CB2+BE2
∴(5![]() )2=(10x)2+(5x)2
)2=(10x)2+(5x)2
∴x=1
∴OA=10=CB,OC=AB=8,AE=3
∴C(0,8) E(10,3) D(6,0)
设直线CE的解析式为y=kx+b
∴![]()
∴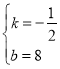
∴![]() ,
,
令y=0,解得:x=16,
∴与x轴交点P的坐标是(16,0)
③存在,
当DM∥CP时
△ODM∽△OPC
∴![]()
∴OM=3
∴M(0,3)
∴![]()
由对称性 M1(0,-3)
∴![]()
当∠OMD=∠OPC时
△OMD∽△OPC
∴![]()
∴OM=12
∴M2(0,12)
∴y=-2x+12
由对称性M3(0,-12)
∴![]()


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
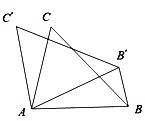
【题目】如图,在△ABC中,∠BAC=75°,以点A为旋转中心,将△ABC绕点A逆时针旋转,得△AB'C',连接BB',若BB'∥AC',则∠BAC′ 的度数是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(﹣1,0);⑤当1<x<4时,有y2<y1,
其中正确的是( )

A. ①②③ B. ①③④ C. ①③⑤ D. ②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产一种节能型灯具并加以销售,现准备在甲市和乙市按不同的方案进行销售,若只在甲市销售,销售价为![]() (元/件),月销售量为
(元/件),月销售量为![]() (件),
(件),![]() 是
是![]() 的一次函数.如表所示,成本为50元/件,无论销售多少,每月还需支出广告费用72500元。设月利润为
的一次函数.如表所示,成本为50元/件,无论销售多少,每月还需支出广告费用72500元。设月利润为![]() (元),(利润=销售额-成本-广告费).若只在乙市销售,销售价为200元/件,受各种因素影响,成本为
(元),(利润=销售额-成本-广告费).若只在乙市销售,销售价为200元/件,受各种因素影响,成本为![]() 元/件(
元/件(![]() 为常数且
为常数且![]() ),当月销售量为
),当月销售量为![]() 件时,每月还需交纳
件时,每月还需交纳![]() 的附加费,设月利润为
的附加费,设月利润为![]() (元).(利润=销售额-成本-附加费)
(元).(利润=销售额-成本-附加费)
月销售量 | 1500 | 2000 |
销售价格 | 185 | 180 |
(1)当![]() 时,
时,![]() ______元/件,
______元/件,![]() ______元(直接写出结果).
______元(直接写出结果).
(2)分别求出![]() 、
、![]() 与
与![]() 的函数关系式(不必写出
的函数关系式(不必写出![]() 的取值范围).
的取值范围).
(3)当![]() 为何值时,
为何值时,![]() 最大?若在乙市销售月利润最大值与甲市最大值相同,求
最大?若在乙市销售月利润最大值与甲市最大值相同,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是等腰直角三角形,∠A=90°,点D是腰AC上的一个动点,过C作CE垂直于BD的延长线,垂足为E.
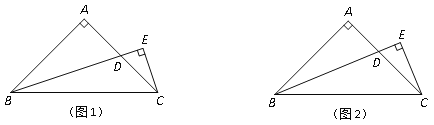
(1)若BD是AC边上的中线,如图1,求![]() 的值;
的值;
(2)若BD是∠ABC的角平分线,如图2,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,⊙O是△ABC外接圆,点D是圆上一点,点D、B分别在AC两侧,且BD=BC,连接AD、BD、OD、CD,延长CB到点P,使∠APB=∠DCB.
(1)求证:AP为⊙O的切线;
(2)若⊙O的半径为1,当△OED是直角三角形时,求△ABC的面积;
(3)若△BOE、△DOE、△AED的面积分别为a、b、c,试探究a、b、c之间的等量关系式,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正比例函数y1=x的图象与反比例函数![]() (k≠0)的图象相交于A、B两点,点A的纵坐标为2.
(k≠0)的图象相交于A、B两点,点A的纵坐标为2.
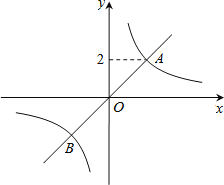
(1)求反比例函数的解析式;
(2)求出点B的坐标,并根据函数图象,写出当y1>y2时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
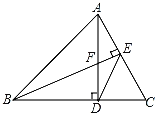
【题目】如图,在△ABC中,AD⊥BC,垂足为D,BE⊥AC,垂足为E,AD与BE相交于点F,连接ED.
(1)求证:△AEF∽△BDF;
(2)若AE=4,BD=8,EF+DF=9,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com