练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    一个多边形的每一个外角为30°，那么这个多边形的边数为____．

    12 【解析】因为多边形的外角和是360°，所以这个多边形的边数为360÷30=12，故答案为12.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：山东省东营市河口区2017-2018学年度第一学期期末考试九年级数学试卷 题型：填空题

    如图，Rt△AOB的一条直角边OB在x轴上，双曲线y=（x>0）经过斜边OA的中点C，与另一直角边交于点D．若S△OCD=9，则S△OBD的值为_______．

    6 【解析】试题分析：过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值，即S=|k|． 【解析】 如图，过C点作CE⊥x轴，垂足为E． ∵Rt△OAB中，∠OBA=90°， ∴CE∥AB， ∵C为Rt△OAB斜边OA的中点C， ∴CE为Rt△OAB的中位线， ∵△OEC∽△OBA， ∴=． ∵双曲线的...

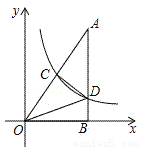
    查看答案和解析>>

    科目：初中数学 来源：北京大学附属中学2017-2018学年七年级上学期期中考试数学试卷 题型：单选题

    在有理数， ， ， 中最大的一个有理数是（ ）

    A. B. C. D.

    D 【解析】试题解析：∵正数负数， ∴． 故在有理数， ， ， 中最大的一个有理数是1. 故选D.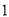

    查看答案和解析>>

    科目：初中数学 来源：广东省广州市天河区2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

    如图，点O是等边△ABC内一点，∠AOB=110°，∠BOC=a，以OC为一边作等边△OCD，连接AD.

    (1)求证：△BOC≌△ADC；

    (2)当OA=OD时，求a的值

    （1）证明见解析；（2）110°. 【解析】试题分析：（1）要证明△BOC≌△ADC，已知条件有AC=BC，CO=CD， 试题解析： （1）∵△ABC是等边三角形，△COD是等边三角形， ∴BC=AC，CO=CD，∠ACB=∠OCD=60°， ∴∠BCO=∠ACD， 在△BOC和△ADC中， ， ∴△BOC≌△ADC； （2）当OA=OD时，∠...

    查看答案和解析>>

    科目：初中数学 来源：广东省广州市天河区2017-2018学年八年级上学期期末考试数学试卷 题型：填空题

    如图，点A，B，C在同一直线上，在这条直线同侧作等边△ABD和等边△BCE，连接AE和CD，交点为M，AE交BD于点P，CD交BE于点Q，连接PQ、BM， 有4个结论：①△ABE≌△DBC，②△DQB≌△ABP，③∠EAC=30°，④∠AMC=120°，请将所有正确结论的序号填在横线上______.

    ①②④ 【解析】∵等边△ABD，等边△EBC，∴AB=BD=AD，BE=BC=EC，∠ABD=∠EBC=60°， ∴∠ABE=∠DBC，∠DBE=60°， 在△ABE和△DBC中， ， ∴△ABE≌△DBC，①说法正确； 由①可得：∠PAB=∠QDB， 在△DQB和△ABP中， ， ∴△DQB≌△ABP，②说法正确； ③说法不能证明，错误...

    查看答案和解析>>

    科目：初中数学 来源：广东省广州市天河区2017-2018学年八年级上学期期末考试数学试卷 题型：单选题

    若分式有意义，则（ ）

    A. x≠1 B. x≠0 C. x≠-1 D. x≠±1

    A 【解析】由题意得：x－1≠0，即x≠1. 故选A.

    查看答案和解析>>

    科目：初中数学 来源：江苏省东部分校2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

    某超市准备购进A、B两种品牌台灯，其中A每盏进价比B进价贵30元，A售价120元，B售价80元.已知用1040元购进的A数量与用650元购进B的数量相同.

    （1）求A、B的进价；

    （2）超市打算购进A、B台灯共100盏，要求A、B的总利润不得少于3400元，不得多于3550元，问有多少种进货方案？

    （3）在（2）的条件下，该超市决定对A进行降价促销，A台灯每盏降价m（8＜m＜15）元，B不变，超市如何进货获利最大？

    （1）A进价80元，B进价50元；（2）16种；（3）当8

    查看答案和解析>>

    科目：初中数学 来源：江苏省东部分校2017-2018学年八年级上学期期末考试数学试卷 题型：填空题

    人的眼睛可以看见的红光的波长为0.000077cm,用科学记数法精确到0.00001cm表示为____cm.

    8×10－５ 【解析】试题解析：0.000077≈0.00008=8×10-5． 故答案为：8×10-5．

    查看答案和解析>>

    科目：初中数学 来源：江西省萍乡市2017-2018学年七年级上学期期末考试数学试卷 题型：解答题

    先化简，再求值：2（3x2－2x+1）－5（－2x2－7x），其中x=－1．

    ，－13． 【解析】试题分析：去括号，合并同类项，把的值代入计算即可. 试题解析：原式 当时， 原式

    查看答案和解析>>

    同步练习册答案