
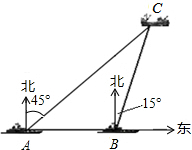
 (2013•遂宁)钓鱼岛自古以来就是我国的神圣领土,为维护国家主权和海洋权利,我国海监和渔政部门对钓鱼岛 海域实现了常态化巡航管理.如图,某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A、B,B船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留根号)
(2013•遂宁)钓鱼岛自古以来就是我国的神圣领土,为维护国家主权和海洋权利,我国海监和渔政部门对钓鱼岛 海域实现了常态化巡航管理.如图,某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A、B,B船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留根号)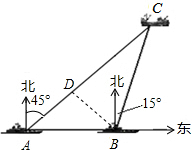 解:过点B作BD⊥AC于D.
解:过点B作BD⊥AC于D.
| ||
| 2 |
| 2 |
| BD |
| sin∠BCD |
10
| ||
|
| 2 |
| 2 |


科目:初中数学 来源: 题型:
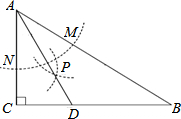 (2013•遂宁)如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于
(2013•遂宁)如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
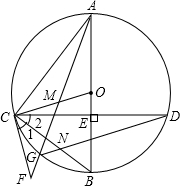 (2013•遂宁)如图,在⊙O中,直径AB⊥CD,垂足为E,点M在OC上,AM的延长线交⊙O于点G,交过C的直线于F,∠1=∠2,连结CB与DG交于点N.
(2013•遂宁)如图,在⊙O中,直径AB⊥CD,垂足为E,点M在OC上,AM的延长线交⊙O于点G,交过C的直线于F,∠1=∠2,连结CB与DG交于点N.| 1 | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com