
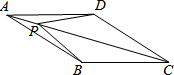
 如图,菱形ABCD的对角线AC上有一动点P,BC=6,∠ABC=150°,则线段AP+BP+PD的最小值为6$\sqrt{2}$.
如图,菱形ABCD的对角线AC上有一动点P,BC=6,∠ABC=150°,则线段AP+BP+PD的最小值为6$\sqrt{2}$. 分析 将△ADC逆时针旋转60°,得到△AD′C′,连接BD′交AC于P,交AC′于E,连接PD,求出BD′,证明PA=PE,PD=ED′,根据两点之间线段最短得到答案.
解答  解:将△ADC逆时针旋转60°,得到△AD′C′,连接BD′交AC于P,交AC′于E,连接PD,
解:将△ADC逆时针旋转60°,得到△AD′C′,连接BD′交AC于P,交AC′于E,连接PD,
∵∠BAD=30°,∠DAD′=60°,
∴∠BAD′=90°,又AB=AD=AD′,
∴BD′=$\sqrt{A{B}^{2}+AD{′}^{2}}$=6$\sqrt{2}$,
∠ABP=45°,又∠BAP=15°,
∴∠APE=∠PAE=60°,
∴△EAP为等边三角形,
∴PA=PE,
又∵△APD≌△AED′,
∴PD=ED′,
根据两点之间线段最短,
∴AP+BP+PD的最小值=PB+PE+ED′=6$\sqrt{2}$,
故答案为:6$\sqrt{2}$.
点评 本题考查的是菱形的性质、轴对称变换和两点之间线段最短的知识,正确找出辅助线是解题的关键,注意轴对称变换的性质的正确运用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某公司去年年初投资1200万元购买新生产线生产新产品,此外,生产每件该产品还需要成本60元,按规定,该产品售价不得低于100元/件且不超过200元/件,该产品的年销售量y(万件)与产品售价x(元/件)之间的关系如图所示.
某公司去年年初投资1200万元购买新生产线生产新产品,此外,生产每件该产品还需要成本60元,按规定,该产品售价不得低于100元/件且不超过200元/件,该产品的年销售量y(万件)与产品售价x(元/件)之间的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直线AC的同侧有Rt△ABD和Rt△BCE,已知∠ABD=∠C=90°,∠A=45°,∠E=30°.若△ABD绕点B顺时针方向旋转,当两个三角形有一边平行时,旋转的角度(小于180°)是( )
如图,直线AC的同侧有Rt△ABD和Rt△BCE,已知∠ABD=∠C=90°,∠A=45°,∠E=30°.若△ABD绕点B顺时针方向旋转,当两个三角形有一边平行时,旋转的角度(小于180°)是( )| A. | 90° | B. | 45° | C. | 45°或90° | D. | 45°或90°或135° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com