Question

6．如图，点E为x轴正半轴上一点，⊙E交x轴于A、B两点，交y轴于C、D两点，P点为劣弧$\widehat{BC}$上一个动点，且A（-1，0），E（1，0）．
（1）如图1，求点C的坐标；
（2）如图2，连接PA，PC．若CQ平分∠PCD交PA于Q点，当P点在运动时，线段AQ的长度是否发生变化；若不变求出其值，若发生变化，求出变化的范围；
（3）如图3，连接PD，当P点在运动时（不与B、C两点重合）$\frac{PC+PD}{PA}$的值是否变化，若不变，求出这个值；若变化，请说明理由．（注：三角形的三边比为1：$\sqrt{3}$：2，那么这个三角形的最小内角为30°．）

Answer 1

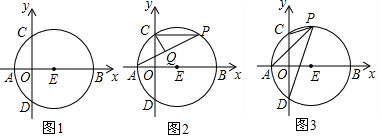
分析 （1）连接EC，则EC=EA=2，然后利用勾股定理就可求出OC的长，从而求出点C的坐标；
（2）不发生变化，连接CB，利用等弧所对的圆周角相等可证明AQ=AC，AC是一个固定值，所以不发生变化．再利用勾股定理就可求出AC的长即是AQ的长；
（3）$\frac{PC+PD}{PA}$的值不变化．证明的时候利用三角形的全等来证明．

解答 解：（1）如图1，连接EC，则EC=EA=2，
∵OE=1，
∴OC=$\sqrt{C{E}^{2}-O{E}^{2}}$，
，故点C的坐标为（0，$\sqrt{3}$）；

（2）不发生变化．
如图2，连接CB，则∠CPA=∠CBA=∠ACO，
∵∠ACQ=∠ACO+∠OCQ，∠AQC=∠CPA+∠PCQ，
∵CQ平分∠PCD，则∠PCQ=∠OCQ，
则∠ACQ=∠AQC，得AQ=AC=2；

（3）结论①不变，在PD的延长线上截取DM=PC，则PC+PD=PM，
如图3，连接AM，
在△PAC和△MAD中
$\left\{\begin{array}{l}{PC=MD}\\{∠PCA=∠ADM}\\{CA=AD}\end{array}\right.$，
∴△PAC≌△MAD（SAS），
∴MA=PA，∠MAP=∠DAC=120°，
则△PAM是以30°为底角的等腰三角形，
∴$\frac{PM}{PA}$=$\frac{PC+PD}{PA}$=$\sqrt{3}$．

点评 本题综合考查了圆的知识，以及全等三角形的判定．所以学生学习时一定要会把所学的知识灵活的运用起来．