
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.

(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.问:此时直线ON是否平分∠AOC?请说明理由.
(2)将图1中的三角板绕点O以每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则 t的值为 秒(直接写出结果).
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,试探索:在旋转过程中,∠AOM与∠NOC的差是否发生变化?若不变,请求出这个差值;若变化,请求出差的变化范围.
【答案】(1)直线ON平分∠AOC;(2)12或30秒;(3)差为定值30°.
【解析】试题分析:(1)直线ON平分∠AOC,设ON的反向延长线为OD,已知OM平分∠BOC,根据角平分线的定义可得∠MOC=∠MOB,又由OM⊥ON,根据垂直的定义可得∠MOD=∠MON=90°,所以∠COD=∠BON,再根据对顶角相等可得∠AOD=∠BON,即可∴∠COD=∠AOD,结论得证;(1)已知∠BOC=120°,根据平角的定义可得∠AOC=60°,旋转至直线ON恰好平分锐角∠AOC,可得旋转120°或300°时ON平分∠AOC,由此可得10t=120°或300°,所以n=12或30;(3)差为定值30°,因为∠MON=90°,∠AOC=60°,所以∠AOM=90°-∠AON,∠NOC=60°-∠AON,再根据角的的和差计算即可.
试题解析:
(1)直线ON平分∠AOC.理由:
设ON的反向延长线为OD,
∵OM平分∠BOC,
∴∠MOC=∠MOB,
又∵OM⊥ON,
∴∠MOD=∠MON=90°,
∴∠COD=∠BON,
又∵∠AOD=∠BON(对顶角相等),
∴∠COD=∠AOD,
∴OD平分∠AOC,即直线ON平分∠AOC.
(2)12或30秒
(3)差为定值30°
∵∠MON=90°,∠AOC=60°,
∴∠AOM=90°-∠AON、∠NOC=60°-∠AON,
∴∠AOM-∠NOC=(90°-∠AON)-(60°-∠AON)=30°.


科目:初中数学 来源: 题型:
【题目】已知整数a1,a2,a3,a4,…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,……以此类推,则a2018的值为( )
A. ﹣1007 B. ﹣1008 C. ﹣1009 D. ﹣2018
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,P为AB上一点,则下列四个条件中, ①∠ACP=∠B②∠APC=∠ACB③ ![]() ④ABCP=APCB ,
④ABCP=APCB ,
其中能满足△APC和△ACB相似的条件有( )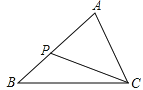
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小兰和小潭分别用掷A、B两枚骰子的方法来确定P(x,y)的位置,她们规定:小兰掷得的点数为x,小谭掷得的点数为y,那么,她们各掷一次所确定的点落在已知直线y=-2x+6上的概率为()
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在同一平面内OA⊥OB,OC是OA绕点O顺时针方向旋转α(α<90°)度得到,OD平分∠BOC,OE平分∠AOC.
(1)若α=60即∠AOC=60°时,求∠BOC,∠DOE.
(2)在α的变化过程中,∠DOE的度数是一个定值吗?若是定值,请求出这个值;若不是定值,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”黄金周期间,小明要与父母外出游玩,带了2件上衣和3条长裤(把衣服和裤子分别装在两个袋子里),上衣颜色有红色、黄色,长裤有红色、黑色、黄色.
问题为:
(1)小明随意拿出一条裤子和一件上衣配成一套,用(画树状图或列表格)中的一种列出所有可能出现结果;
(2)配好一套衣服,小明正好拿到黑色长裤的概率是多少;
(3)他任意拿出一件上衣和一条长裤穿上的颜色正好相同的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具店进了一排黑白塑料球,共5箱,每箱的规格、数量都相同,其中每箱中装有黑白两种颜色的塑料球共3000个,为了估计每箱中两种颜色球的个数,随机抽查了一箱,将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后,发现摸到黑球的概率在0.8附近波动,则此可以估计这批塑料球中黑球的总个数,请将黑球总个数用科学记数法表示约为个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com