
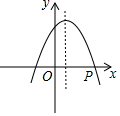
 如图,抛物线y=ax2+bx+c(a<0)的对称轴是过点(1,0)且平行于y轴的直线,若点P(3,0)在该抛物线上,则a-b+c的值为0.
如图,抛物线y=ax2+bx+c(a<0)的对称轴是过点(1,0)且平行于y轴的直线,若点P(3,0)在该抛物线上,则a-b+c的值为0.  学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
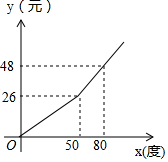 某城市电业局为鼓励居民节约用电,采取按月用电量分段收费办法,居民应交电费y(元)与用电量x(度)的函数关系如图所示.
某城市电业局为鼓励居民节约用电,采取按月用电量分段收费办法,居民应交电费y(元)与用电量x(度)的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
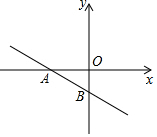 如图,一次函数y=ax+b的图象分别与x轴、y轴的负半轴相交于A、B,则下列结论一定正确的是( )
如图,一次函数y=ax+b的图象分别与x轴、y轴的负半轴相交于A、B,则下列结论一定正确的是( )| A. | a-b>0 | B. | a+b>0 | C. | b-a>0 | D. | -a-b>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
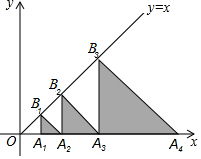 如图,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上,已知OA1=1,则△B2016A2016A2017的面积为24029.
如图,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上,已知OA1=1,则△B2016A2016A2017的面积为24029.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
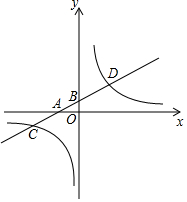 如图,在平面直角坐标系中,一次函数y1=kx+b的图象分别交x轴,y轴于A、B两点,与反比例函数y2=$\frac{n}{x}$的图象交于C、D两点,已知点C的坐标为(-4,-1),点D的横坐标为2.
如图,在平面直角坐标系中,一次函数y1=kx+b的图象分别交x轴,y轴于A、B两点,与反比例函数y2=$\frac{n}{x}$的图象交于C、D两点,已知点C的坐标为(-4,-1),点D的横坐标为2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
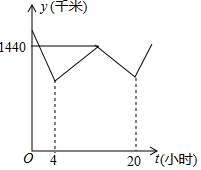 甲、乙两车分别从A、B两地同时出发匀速相向而行,大楼C位于AB之间,甲与乙相遇在AC中点处,然后两车立即掉头,以原速原路返回,直到各自回到出发点.设甲、乙两车距大楼C的距离之和为y(千米),甲车离开A地的时间为t(小时),y与t的函数图象所示,则第21小时时,甲乙两车之间的距离为1350千米.
甲、乙两车分别从A、B两地同时出发匀速相向而行,大楼C位于AB之间,甲与乙相遇在AC中点处,然后两车立即掉头,以原速原路返回,直到各自回到出发点.设甲、乙两车距大楼C的距离之和为y(千米),甲车离开A地的时间为t(小时),y与t的函数图象所示,则第21小时时,甲乙两车之间的距离为1350千米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com