
| B市运往C市机器的数量/台 | 1 | x |
| B市运往D市机器的数量/台 | 5 | 6-x |
| A市运往C市机器的数量/台 | 9 | 10-x |
| A市运往D市机器的数量/台 | 3 | 2+x |
| B市运往C市机器的数量/台 | 1 | x |
| B市运往C市机器的运费/元 | 300 | 300x |
| B市运往D市机器的运费/元 | 500 | 500(6-x) |
| A市运往C市机器的运费/元 | 400 | 400(10-x) |
| A市运往D市机器的运费/元 | 800 | 800(2+x) |
分析 (1)根据题意和表格中的数据可以将表一和表二补充完整;
(2)根据表格中的数据可以表示出总的运输费用,然后根据题目中的数据和一次函数的性质,可以求得最低运输费用和此种情况下的调运方案.
解答 解:(1)由题意可得,
当B市运往C市机器为x台时,
则B市运往D市机器为(6-x)台,A市运往C市机器为(10-x)台,A市运往D市机器为:8-(6-x)=8-6+x=(2+x)台,
当B市运往C市机器为x台时,
则 B市运往C市机器的运费为300x元,B市运往D市机器的运费为500(6-x)元,A市运往C市机器的运费为:400(10-x)元,A市运往D市机器的运费800(2+x)元,
故答案为:表一:6-x,10-x,2+x;表二:300x,500(6-x),400(10-x),800(2+x);
(2)设从B市运往C市机器x台,总运费为y元,
y=300x+500(6-x)+400(10-x)+800(2+x)=200x+8600,
∵0≤6-x≤6,得0≤x≤6,
∴10-x>0,
∵y=200x+8600,
∴当x=0时,y取得最小值,此时y=8600,
即使得总运费最低的方案是:B市运往C市机器为0台,B市运往D市机器为6台,A市运往C市机器为10台,A市运往D市机器2台,此时总运费为8600元.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用一次函数的性质解答问题,求出相应的最值.


科目:初中数学 来源: 题型:填空题
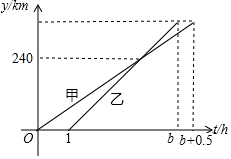 甲、乙两车从A地出发前往B地.在整个行程中,甲、乙两车离开A地的距离 y(km)与行驶的时间t(h)的关系如图所示,则A、B两地的距离为360km.
甲、乙两车从A地出发前往B地.在整个行程中,甲、乙两车离开A地的距离 y(km)与行驶的时间t(h)的关系如图所示,则A、B两地的距离为360km.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
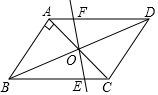 如图,平行四边形ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
如图,平行四边形ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD是对角线互相垂直的四边形,且OB=OD,请你添加一个适当的条件OA=OC,使四边形ABCD是菱形.(只需添加一个即可)
如图,四边形ABCD是对角线互相垂直的四边形,且OB=OD,请你添加一个适当的条件OA=OC,使四边形ABCD是菱形.(只需添加一个即可)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
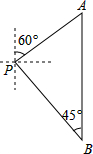 如图,一辆汽车从P处出发,先沿北偏东60°的方向行驶到达A处后,接着向正南方向行驶100($\sqrt{3}$+1)千米到达B处.在B处观测到出发时所在的P处在北偏西45°方向上,P,A两处相距多少千米?
如图,一辆汽车从P处出发,先沿北偏东60°的方向行驶到达A处后,接着向正南方向行驶100($\sqrt{3}$+1)千米到达B处.在B处观测到出发时所在的P处在北偏西45°方向上,P,A两处相距多少千米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com