
【题目】如图,甲、丙两地相距500km,一列快车从甲地驶往丙地,途中经过乙地;一列慢车从乙地驶往丙地,两车同时出发,同向而行,折线ABCD表示两车之间的距离y(km)与慢车行驶的时间为x(h)之间的函数关系.根据图中提供的信息,下列说法不正确的是( )
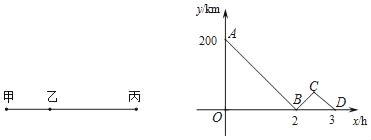
A. 甲、乙两地之间的距离为200 kmB. 快车从甲地驶到丙地共用了2.5 h
C. 快车速度是慢车速度的1.5倍D. 快车到达丙地时,慢车距丙地还有50 km
【答案】C
【解析】
根据两车同时出发,同向而行,所以点A即为甲、乙两地的距离;图中点B为y=0,即快慢两车的距离为0,所以B表示快慢两车相遇的时间;由图像可知慢车走300km,用了3小时,可求出慢车的速度,进而求出快车的速度;点C的横坐标表示快车走到丙地用的时间,根据快车与慢车的速度,可求出点C的坐标
A、由图像分析得,点A即为甲、乙两地的距离,即甲、乙两地之间的距离为![]() 选项A是正确
选项A是正确
BC、由图像可知慢车走300km,用了3小时,则慢车的速度为100km/h,因为1h快车比慢车多走100km,故快车速度为200km/h,所以快车从甲地到丙地的时间=500![]() 200=2.5h,故选项B是正确的,快车速度是慢车速度的两倍,故选项C是错误的
200=2.5h,故选项B是正确的,快车速度是慢车速度的两倍,故选项C是错误的
D、快车从甲地驶到丙地共用了2.5h,即点C的横坐标2.5,则慢车还剩0.5h才能到丙地,距离=0.5![]() 100=50km,故快车到达丙地时,慢车距丙地还有50km,选项D是正确的
100=50km,故快车到达丙地时,慢车距丙地还有50km,选项D是正确的
故正确答案为C


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】若抛物线上![]() ,它与
,它与![]() 轴交于
轴交于![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() ,
,![]() 是抛物线上
是抛物线上![]() 、
、![]() 之间的一点,
之间的一点,
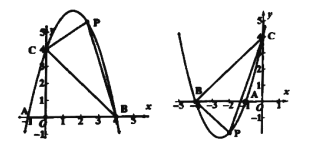
(1)当![]() 时,求抛物线的方程,并求出当
时,求抛物线的方程,并求出当![]() 面积最大时的
面积最大时的![]() 的横坐标。
的横坐标。
(2)当![]() 时,求抛物线的方程及
时,求抛物线的方程及![]() 的坐标,并求当
的坐标,并求当![]() 面积最大时
面积最大时![]() 的横坐标。
的横坐标。
(3)根据(1)、(2)推断![]() 的横坐标与
的横坐标与![]() 的横坐标有何关系?
的横坐标有何关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
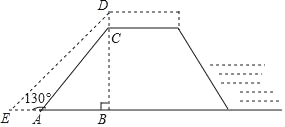
【题目】为做好防汛工作,防汛指挥部决定对某水库的水坝进行加高加固,专家提供的方案是:水坝加高2米(即CD=2米),背水坡DE的坡度i=1:1(即DB:EB=1:1),如图所示,已知AE=4米,∠EAC=130°,求水坝原来的高度BC.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售单价分别为![]() 元/筒、
元/筒、![]() 元/筒的甲、乙两种羽毛球.根据消费者需求,该网店决定用不超过
元/筒的甲、乙两种羽毛球.根据消费者需求,该网店决定用不超过![]() 元购进甲、乙两种羽毛球共
元购进甲、乙两种羽毛球共![]() 简.且甲种羽毛球的数量大于乙种羽毛球数量的
简.且甲种羽毛球的数量大于乙种羽毛球数量的![]() .已知甲、乙两种羽毛球的进价分别为
.已知甲、乙两种羽毛球的进价分别为![]() 元/筒、
元/筒、![]() 元/筒。若设购进甲种羽毛球
元/筒。若设购进甲种羽毛球![]() 简.
简.
(1)该网店共有几种进货方案?
(2)若所购进羽毛球均可全部售出,求该网店所获利润![]() (元)与甲种羽毛球进货量
(元)与甲种羽毛球进货量![]() (简)之间的函数关系式,并求利润的最大值
(简)之间的函数关系式,并求利润的最大值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是
A. “明天降雨的概率是80%”表示明天有80%的时间都在降雨
B. “抛一枚硬币正面朝上的概率为![]() ”表示每抛2次就有一次正面朝上
”表示每抛2次就有一次正面朝上
C. “彩票中奖的概率为1%”表示买100张彩票肯定会中奖
D. “抛一枚正方体骰子,朝上的点数为2的概率为![]() ”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在![]() 附近
附近
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备从甲乙两位选手中选择一位选手代表学校参加所在地区的汉字听写大赛,学校对两位选手从表达能力、阅读理解、综合素质和汉字听写四个方面做了测试,他们各自的成绩(百分制)如表:
选手 | 表达能力 | 阅读理解 | 综合素质 | 汉字听写 |
甲 | 85 | 78 | 85 | 73 |
乙 | 73 | 80 | 82 | 83 |
(1)由表中成绩已算得甲的平均成绩为80.25,请计算乙的平均成绩,从他们的这一成绩看,应选派谁;
(2)如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们2、1、3和4的权,请分别计算两名选手的平均成绩,从他们的这一成绩看,应选派谁.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
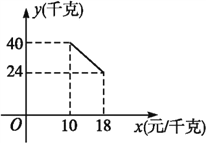
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求每天的销售利润W(元)与销售价x(元/千克)之间的函数关系式.当销售价为多少时,每天的销售利润最大?最大利润是多少?
(3)该经销商想要每天获得168元的销售利润,销售价应定为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
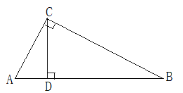
【题目】如图,在△ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm.
(1)求△ABC的面积;
(2)求CD的长;
(3)作出△ABC的边AC上的中线BE,并求出△ABE的面积;
(4)作出△BCD的边BC上的高DF,当BD=![]() 时,试求出DF的长(用
时,试求出DF的长(用![]() 表示).
表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com