
【题目】点P,Q在数轴上分别表示的数分别为p,q,我们把p,q之差的绝对值叫做点P,Q之间的距离,即![]() .如图,在数轴上,点A,B,O,C,D的位置如图所示,则
.如图,在数轴上,点A,B,O,C,D的位置如图所示,则![]() ;
;![]() ;
;![]() .请探索下列问题:
.请探索下列问题:
![]()
(1)计算![]() ____________,它表示哪两个点之间的距离?________________________.
____________,它表示哪两个点之间的距离?________________________.
(2)点M为数轴上一点,它所表示的数为x,用含x的式子表示PB=____________;当PB=2时,x=____________;当x=____________时,|x+4|+|x-1|+|x-3|的值最小.
(3)|x-1|+|x-2|+|x-3|+…+|x-2018|+|x-2019|的最小值为________________________.
【答案】(1)5;A与C;(2)|x+2|;-4或0;1;(3)1019090
【解析】
(1)由所给信息,结合绝对值的性质可求;
(2)由绝对值的性质,分段去掉绝对值符号,在不同的x范围内确定|x+4|+|x1|+|x3|的最小值;
(3)由所给式子的对称性,结合绝对值的性质,将所求绝对值式子转化为求0+2+4+…+2018的和.
(1)|1(4)|=|1+4|=|5|=5,|1(4)|表示点A与C之间的距离,
故答案为:5,点A与C;
(2)∵点P为数轴上一点,它所表示的数为x,点B表示的数为2,
∴PB=|x(2)|=|x+2|,
当PB=2时,|x+2|=2,得x=0或x=4,
当x≤4时,|x+4|+|x1|+|x3|=x4+1x+3x=x≥4;
当4<x<1时,|x+4|+|x1|+|x3|=x+4+1x+3x=8x,
当1≤x≤3时,|x+4|+|x1|+|x3|=x+4+x1+3x=6+x,
当x>3时,|x+4|+|x1|+|x3|=x+4+x1+x3=3x>9,
∴当x=1时,|x+4|+|x1|+|x3|有最小值;
故答案为:|x+2|;4或0;1
(3)|x1|+|x2019|≥|12019|=2018,
当且仅当1≤x≤2019时,|x1|+|x2019|=2018,
当且仅当2≤x≤2018时,|x2|+|x2018|≥|22018|=2016,
…
同理,当且仅当1009≤x≤1011时,|x1009|+|x1011|≥|10091011|=2,
|x1010|≥0,当x=1010时,|x1010|=0,
∴|x1|+|x2|+|x3|+…+|x2018|+|x2019|≥0+2+4+…+2018=1019090,
∴|x1|+|x2|+|x3|+…+|x2018|+|x2019|的最小值为1019090;
故答案为1019090.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某县教育局为了丰富初中学生的大课间活动,要求各学校开展形式多样的阳光体育活动.某中学就“学生体育活动兴趣爱好”的问题,随机调查了本校某班的学生,并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图:

(1)在这次调查中,喜欢篮球项目的同学有 人,在扇形统计图中,“乒乓球”的百分比为 %,如果学校有800名学生,估计全校学生中有 人喜欢篮球项目.
(2)请将条形统计图补充完整.
(3)在被调查的学生中,喜欢篮球的有2名女同学,其余为男同学.现要从中随机抽取2名同学代表班级参加校篮球队,请直接写出所抽取的2名同学恰好是1名女同学和1名男同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种货车,![]() 辆大货车与
辆大货车与![]() 辆小火车一次可以运货
辆小火车一次可以运货![]() 吨,
吨,![]() 辆大货车与
辆大货车与![]() 辆小货车一次可以运货
辆小货车一次可以运货![]() 吨.
吨.
(1)求![]() 辆大货车和
辆大货车和![]() 辆小货车一次可以分别运多少吨;
辆小货车一次可以分别运多少吨;
(2)现有![]() 吨货物需要运输,货运公司拟安排大小货车共
吨货物需要运输,货运公司拟安排大小货车共![]() 辆把全部货物一次运完.求至少需要安排几辆大货车?
辆把全部货物一次运完.求至少需要安排几辆大货车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 某单位在二月份准备组织部分员工到北京旅游,现联系了甲、乙两家旅行社,两家旅行社报价均为2000元/人,两家旅行社同时都对10人以上的团体推出了优惠举措:甲旅行社对每位员工七五折优惠;而乙旅行社是免去一位带队管理员工的费用,其余员工八折优惠.
(1)如果设参加旅游的员工共有a(a![]() )人,则甲旅行社的费用为 元,乙旅行社的费用为 元;(用含a的代数式表示,并化简.)
)人,则甲旅行社的费用为 元,乙旅行社的费用为 元;(用含a的代数式表示,并化简.)
(2)假如这个单位现组织包括管理员工在内的共20名员工到北京旅游,该单位选择哪一家旅行社比较优惠?请说明理由;
(3)如果计划在二月份外出旅游七天,设最中间一天的日期为m.
①这七天的日期之和为 ;(用含m的代数式表示,并化简.)
②假如这七天的日期之和为63的倍数,则他们可能于二月几号出发?(写出所有符合条件的可能性,并写出简单的计算过程.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡镇实施产业扶贫,帮助贫困户承包了荒山种植蜜柚,已知该蜜柚的成本价为8元/千克。
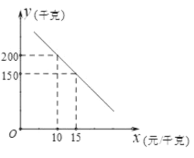
到了收获季节,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销量
干克)与销售单价x(元/千克)之间的函数关系如图所示.
(1)求y与x的函数关系式,并写出x的取值范围:
(2)当该蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
(3)某农户今年共采摘蜜柚4800千克,该蜜柚的保持期为40天,根据(2)中获得最大利润的方式进行销售,能否销售完这批蜜柚?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
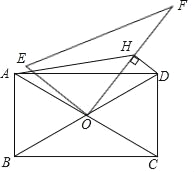
【题目】如图,在矩形ABCD中,AB=4,BC=4![]() ,对角线AC、BD相交于点O,现将一个直角三角板OEF的直角顶点与O重合,再绕着O点转动三角板,并过点D作DH⊥OF于点H,连接AH.在转动的过程中,AH的最小值为_____.
,对角线AC、BD相交于点O,现将一个直角三角板OEF的直角顶点与O重合,再绕着O点转动三角板,并过点D作DH⊥OF于点H,连接AH.在转动的过程中,AH的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
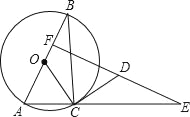
【题目】如图,⊙O是Rt△ABC的外接圆,AB为直径,∠ABC=30°,CD是⊙O的切线,ED⊥AB于F,
(1)求证:△CDE是等腰三角形;
(2)若AB=4,![]() ,求证:△OBC≌△DCE.
,求证:△OBC≌△DCE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=ax+b的图象过点(﹣2,1),则关于抛物线y=ax2﹣bx+3的三条叙述:其中所有正确叙述的个数是( )
①过点(2,1),②对称轴可以是x=1,③当a<0时,其顶点的纵坐标的最小值为3.
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com