
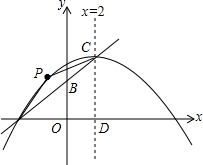
 在平面直角坐标系中,A(-4,0),B(0,2),直线x=2与直线AB交于点C,与x轴交于点D,抛物线经过点A,且以C为顶点.
在平面直角坐标系中,A(-4,0),B(0,2),直线x=2与直线AB交于点C,与x轴交于点D,抛物线经过点A,且以C为顶点.分析 (1)先求出直线AB以及顶点C坐标,再利用顶点式求出抛物线解析式即可.
(2)连接PD,设点P(m,-$\frac{1}{12}$m2+$\frac{1}{3}$m+$\frac{8}{3}$),根据S△PAC=S△PAD+S△PCD-S△ACD构建二次函数,利用二次函数性质解决最值问题.
解答 解:(1)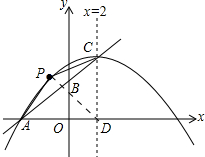 设直线AB为y=kx+b,则有$\left\{\begin{array}{l}{b=2}\\{-4k+b=0}\end{array}\right.$解得$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=2}\end{array}\right.$,
设直线AB为y=kx+b,则有$\left\{\begin{array}{l}{b=2}\\{-4k+b=0}\end{array}\right.$解得$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=2}\end{array}\right.$,
∴直线AB为y=$\frac{1}{2}$x+2,由题意点C(2,3),
设抛物线为y=a(x-2)2+3,点A(-4,0)代入得到a=-$\frac{1}{12}$,
∴抛物线解析式为y=-$\frac{1}{12}$(x-2)2+3,即y=-$\frac{1}{12}$x2+$\frac{1}{3}$x+$\frac{8}{3}$.
(2)连接PD,设点P(m,-$\frac{1}{12}$m2+$\frac{1}{3}$m+$\frac{8}{3}$),
∴S△PAC=S△PAD+S△PCD-S△ACD=$\frac{1}{2}$•6•(-$\frac{1}{12}$m2+$\frac{1}{3}$m+$\frac{8}{3}$)+$\frac{1}{2}$•3•(2-m)-$\frac{1}{2}$•6•3=-$\frac{1}{4}$m2-$\frac{1}{2}$m+2=-$\frac{1}{4}$(m+1)2+$\frac{9}{4}$.
∵a=-$\frac{1}{4}$<0,
∴m=-1时,S△PAC的最大值为$\frac{9}{4}$.
点评 本题考查抛物线与x轴的交点、一次函数、三角形面积等知识,解题的关键是熟练掌握待定系数法确定函数解析式,学会分割法求三角形面积,属于中考常考题型.


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:解答题
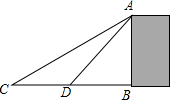 天下第一门-华门,位于山西省临汾市尧都区尧庙广场的西面,是一座纪念华夏文明的门.周日,小韬与同学一起来到华门前游玩,他想通过测量来计算华门的高度,于是他借来测角仪和卷尺,如图,他在点C处测得华门AB顶端A的仰角为30°,沿着CB方向向华门行进了36.6米到达点D处,测得华门AB顶端A的仰角为45°,求华门AB的高为多少?(结果保留整数,参考数据$\sqrt{3}$≈1.73)
天下第一门-华门,位于山西省临汾市尧都区尧庙广场的西面,是一座纪念华夏文明的门.周日,小韬与同学一起来到华门前游玩,他想通过测量来计算华门的高度,于是他借来测角仪和卷尺,如图,他在点C处测得华门AB顶端A的仰角为30°,沿着CB方向向华门行进了36.6米到达点D处,测得华门AB顶端A的仰角为45°,求华门AB的高为多少?(结果保留整数,参考数据$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
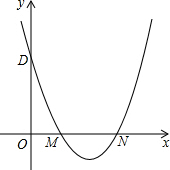 抛物线y=x2-4x+3交x轴于M,N点(M点在N点左边),交y轴于D点,点E为第一象限抛物线上的点,若∠EMN=2∠ODM,求E点坐标.
抛物线y=x2-4x+3交x轴于M,N点(M点在N点左边),交y轴于D点,点E为第一象限抛物线上的点,若∠EMN=2∠ODM,求E点坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
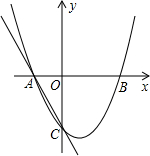 如图,抛物线y=ax2+bx+c与x轴交于A(-1,0)、B(2,0)两点,与y轴交于点C(0,-2),过A、C画直线.
如图,抛物线y=ax2+bx+c与x轴交于A(-1,0)、B(2,0)两点,与y轴交于点C(0,-2),过A、C画直线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com