练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图所示的图形以点O为旋转中心，旋转________后能与原来的图形重合。

     

     

    【答案】

    60°或120°或180°　

    【解析】

    试题分析：根据旋转对称图形的概念计算出角度即可．

    该图形被平分成六部分，因而每部分被分成的圆心角是60°，

    并且圆具有旋转不变性，因而旋转60度的整数倍，就可以与自身重合．

    故填60°或120°或180°　．

    考点：本题考查了图形的旋转变化

    点评：解答本题的关键是掌握把一个图形绕着一个定点旋转一个角度后，与初始图形重合，这种图形叫做旋转对称图形，这个定点叫做旋转对称中心，旋转的角度叫做旋转角。

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图①，某产品标志的截面图形由一个等腰梯形和抛物线的一部分组成，在等腰梯形ABCD中，AB∥DC，AB=20cm，DC=30CM，∠ADC=45度．对于抛物线部分，其顶点为CD的中点O，且过A、B两点，开口终端的连线MN平行且等于DC．
    （1）如图①所示，在以点O为原点，直线OC为x轴的坐标系内，点C的坐标为（15，0），试求A、B两点的坐标；
    （2）求标志的高度（即标志的最高点到梯形下底所在直线的距离）；
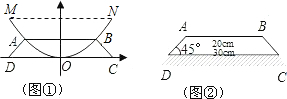    （3）现根据实际情况，需在标志截面图形的梯形部分的外围均匀镀上一层厚度为3c精英家教网m的保护膜，如图②，请在图中补充完整镀膜部分的示意图，并求出镀膜的外围周长．

    查看答案和解析>>

    科目：初中数学 来源：第34章《二次函数》中考题集（36）：34.4 二次函数的应用（解析版） 题型：解答题

    如图①，某产品标志的截面图形由一个等腰梯形和抛物线的一部分组成，在等腰梯形ABCD中，AB∥DC，AB=20cm，DC=30CM，∠ADC=45度．对于抛物线部分，其顶点为CD的中点O，且过A、B两点，开口终端的连线MN平行且等于DC．
    （1）如图①所示，在以点O为原点，直线OC为x轴的坐标系内，点C的坐标为（15，0），试求A、B两点的坐标；
    （2）求标志的高度（即标志的最高点到梯形下底所在直线的距离）；
    （3）现根据实际情况，需在标志截面图形的梯形部分的外围均匀镀上一层厚度为3cm的保护膜，如图②，请在图中补充完整镀膜部分的示意图，并求出镀膜的外围周长．

    查看答案和解析>>

    科目：初中数学 来源：第2章《二次函数》中考题集（34）：2.4 二次函数的应用（解析版） 题型：解答题

    如图①，某产品标志的截面图形由一个等腰梯形和抛物线的一部分组成，在等腰梯形ABCD中，AB∥DC，AB=20cm，DC=30CM，∠ADC=45度．对于抛物线部分，其顶点为CD的中点O，且过A、B两点，开口终端的连线MN平行且等于DC．
    （1）如图①所示，在以点O为原点，直线OC为x轴的坐标系内，点C的坐标为（15，0），试求A、B两点的坐标；
    （2）求标志的高度（即标志的最高点到梯形下底所在直线的距离）；
    （3）现根据实际情况，需在标志截面图形的梯形部分的外围均匀镀上一层厚度为3cm的保护膜，如图②，请在图中补充完整镀膜部分的示意图，并求出镀膜的外围周长．

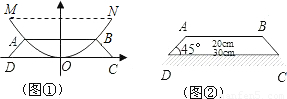
    查看答案和解析>>

    科目：初中数学 来源：2012年重庆市万州区长岭初中中考数学模拟试卷（三）（解析版） 题型：解答题

    如图①，某产品标志的截面图形由一个等腰梯形和抛物线的一部分组成，在等腰梯形ABCD中，AB∥DC，AB=20cm，DC=30CM，∠ADC=45度．对于抛物线部分，其顶点为CD的中点O，且过A、B两点，开口终端的连线MN平行且等于DC．
    （1）如图①所示，在以点O为原点，直线OC为x轴的坐标系内，点C的坐标为（15，0），试求A、B两点的坐标；
    （2）求标志的高度（即标志的最高点到梯形下底所在直线的距离）；
    （3）现根据实际情况，需在标志截面图形的梯形部分的外围均匀镀上一层厚度为3cm的保护膜，如图②，请在图中补充完整镀膜部分的示意图，并求出镀膜的外围周长．

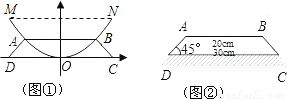
    查看答案和解析>>

    同步练习册答案